8  Bazinio R grafikos įvadas - funkcija plot() ir jos metodai

R grafinė sistema yra labai lanksti ir galinga, turinti įvairių paketų duomenų vizualizavimui, tačiau pradžioje
geriausia pradėti nuo bazinio grafikos paketo. Jame naudojamos funkcijos leidžia kurti tiek paprastus, tiek sudėtingus grafikus, juos pamažu papildant įvairiais elementais.

R grafinės funkcijos skirstomos į dvi pagrindines grupes:

• aukšto lygio funkcijos sukuria naują grafiką su visais pagrindiniais elementais (ašimis, antrašte ir kt.),

• žemo lygio funkcijos prideda papildomus elementus (taškus, linijas, tekstą) prie jau esančio grafiko.

8.1 Funkcija plot()

Didelę dalį dažniausiai naudojamų grafikų galima nubraižyti naudojant aukšto lygio funkciją plot(). Ji yra bendro (generic) pobūdžio funkcija, t.y. jos veiksena priklauso nuo perduoto objekto tipo su kuriuo atliekamas skirtingas vaizdavimo metodas.

Pradėsime nuo plot.default() metodo, kuris sudaro taškų su koordinatėmis \(x\) (abscisė) ir \(y\) (ordinatė) sklaidos diagramą.

x <- -5:15
y <- x^3 - 10*x^2 - 10*x + 3
plot(x = x , y = y) 

Prisiminkite, kad išvardinant parametrus jų eiliškumą galima keisti. Kai parametrai nurodomi iš eilės nustatyta tvarka - jų pavadinimų galima nerašyti.

plot(y = y, x = x)
plot(x, y)

Diagramos išvaizdą galima pakeisti nurodant kitas parametrų reikšmes. Dažniausiai naudojami šie parametrai:

• type – sklaidos diagramos tipas,
• pch – taško simbolis,
• cex – taško simbolio dydis,
• lty – linijos tipas,
• lwd – linijos storis,
• col – taško arba linijos spalva.

Diagramos tipas: parametras type

Peržiūrėsime, kaip keičiant parametro type reikšmę, gaunami skirtingi sklaidos diagramos variantai, kurie skiriasi taškų (\(x\), \(y\)) atvaizdavimo ir jų sujungimo būdais:

• p – diagramoje atidedami nesujungti taškai (numatytasis),
• l – nubraižoma taškus jungianti laužtė,
• b – taškai sujungiami tiesės atkarpomis,
• c – tušti taškai sujungiami tiesės atkarpomis,
• o – braižomi ir taškai, ir juos jungianti laužtė,
• s, S - laiptuotos laužtės,
• h – taškuose \(x\) atidedami \(y\) aukščio stulpeliai,
• n – grafikas be taškų, tik suformuojamos ašys.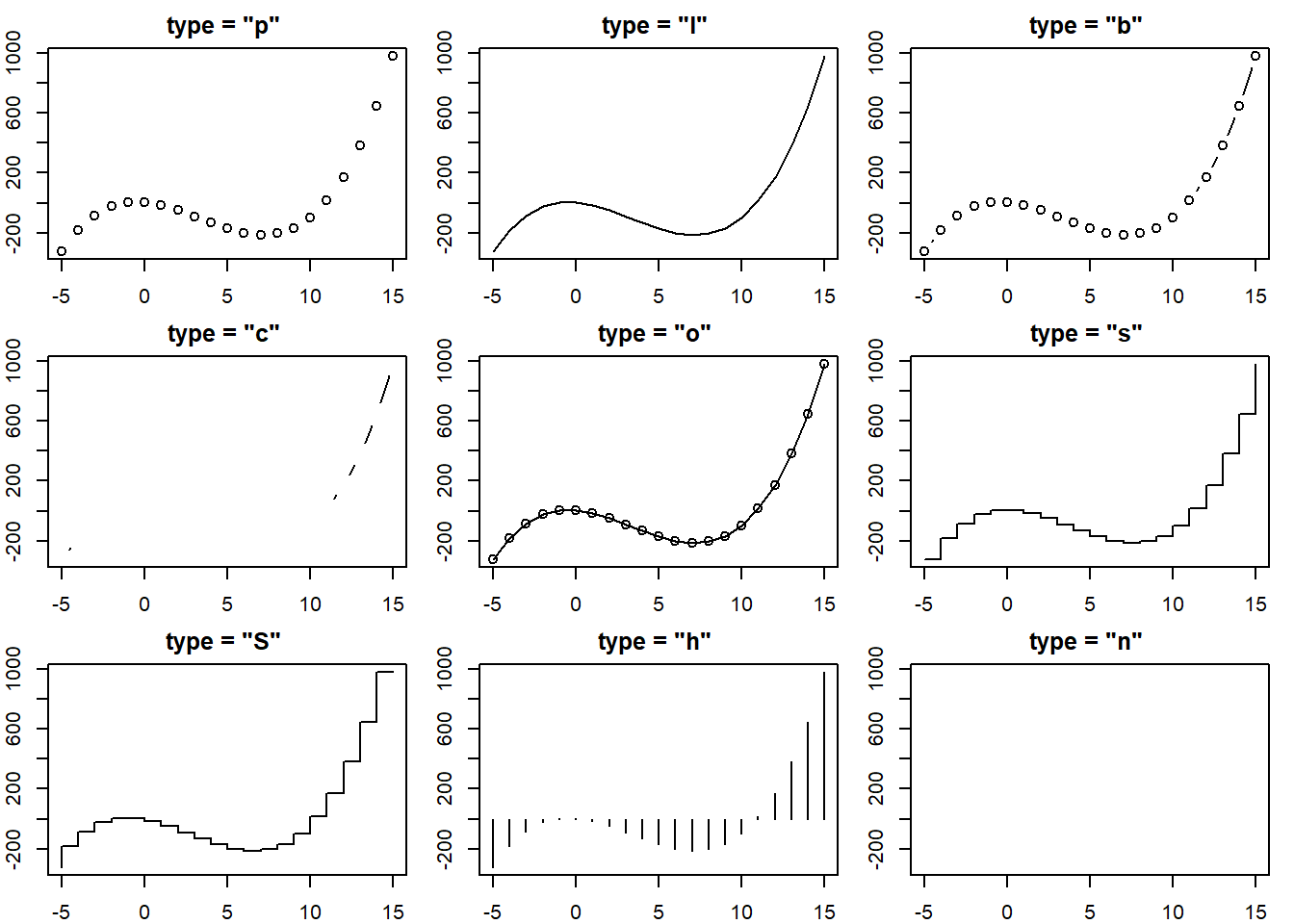

Taškų simboliai: pch, cex, col, bg

Peržvelgsime kai kurių taško simbolio vaizdavimo parametrus:

• pch -– taško simbolis: 0–25 – standartiniai, 32–127 – ASCII simboliai; taip pat galima naudoti tekstą: pch = "*",
• cex -– simbolio dydis: cex > 1 padidina, cex < 1 sumažina,
• col -– taško arba linijos spalva: pagal pavadinimą col = "red" ar spalvos numerį col = 2,
• bg -– simbolio užpildymo spalva (naudojamas su pch nuo 21 iki 25 reikšmės).

Spalvų paletę galima patikrinti su funkcija colors(). Iš viso yra numatytos 657 spalvos. Šiuo atveju peržiūrėsime pirmasias 10 spalvų.

colors()[1:10]
#>  [1] "white"         "aliceblue"     "antiquewhite"  "antiquewhite1"
#>  [5] "antiquewhite2" "antiquewhite3" "antiquewhite4" "aquamarine"   
#>  [9] "aquamarine1"   "aquamarine2"

Spalvas galima nurodyti pagal jos numerį, arba pavadinimą prieš tai nurodytoje paletėje. Alternatyvus spalvos parinkimas - šešioliktainės (angl. hexadecimal) sistemos numeris, pvz. baltą spalvą atitinką numeris #FFFFFF.

Pavyzdžiui, nubrėšime pusantro karto padidintų mėlynų taškų pavaizduotų neužpildytais trikampiais sklaidos diagramą.

plot(x, y, pch = 2, col = "blue", cex = 1.5)

Štai dar vienas įvairių parametrų reikšmių parinkimo pavyzdys.

plot(x, y, pch = 21, col = "black", bg = "orange")

Parametrų, ir jų reikšmių sąrašą nesunkiai galima rasti internete, pavyzdžiui šiame arba kitame puslapyje.

Svarbu paminėti, jog galima nurodyti ne vieną parametro reikšmę, t.y. galima nurodyti visą parametro reikšmių vektorių. Jeigu vektorius yra tokio pat ilgio kaip ir taškų (\(x\), \(y\)) skaičius, tai kiekvienam taškui tam tikro parametro reikšmė bus paimta iš nurodyto vektoriaus. Jeigu vektoriaus ilgis mažesnis už taškų skaičių, tai toks vektorius cikliškai atkartojamas iki taškų skaičiaus ilgio.

Pavyzdžiui, parametrui pch suteiksime dvi reikšmes, kurios cikliškai bus pakartojamos. Taškai su nelyginiu indeksu įgys reikšmę pch = 1, o lyginiai indeksai - pch = 2.

plot(x, y, pch = 1:2)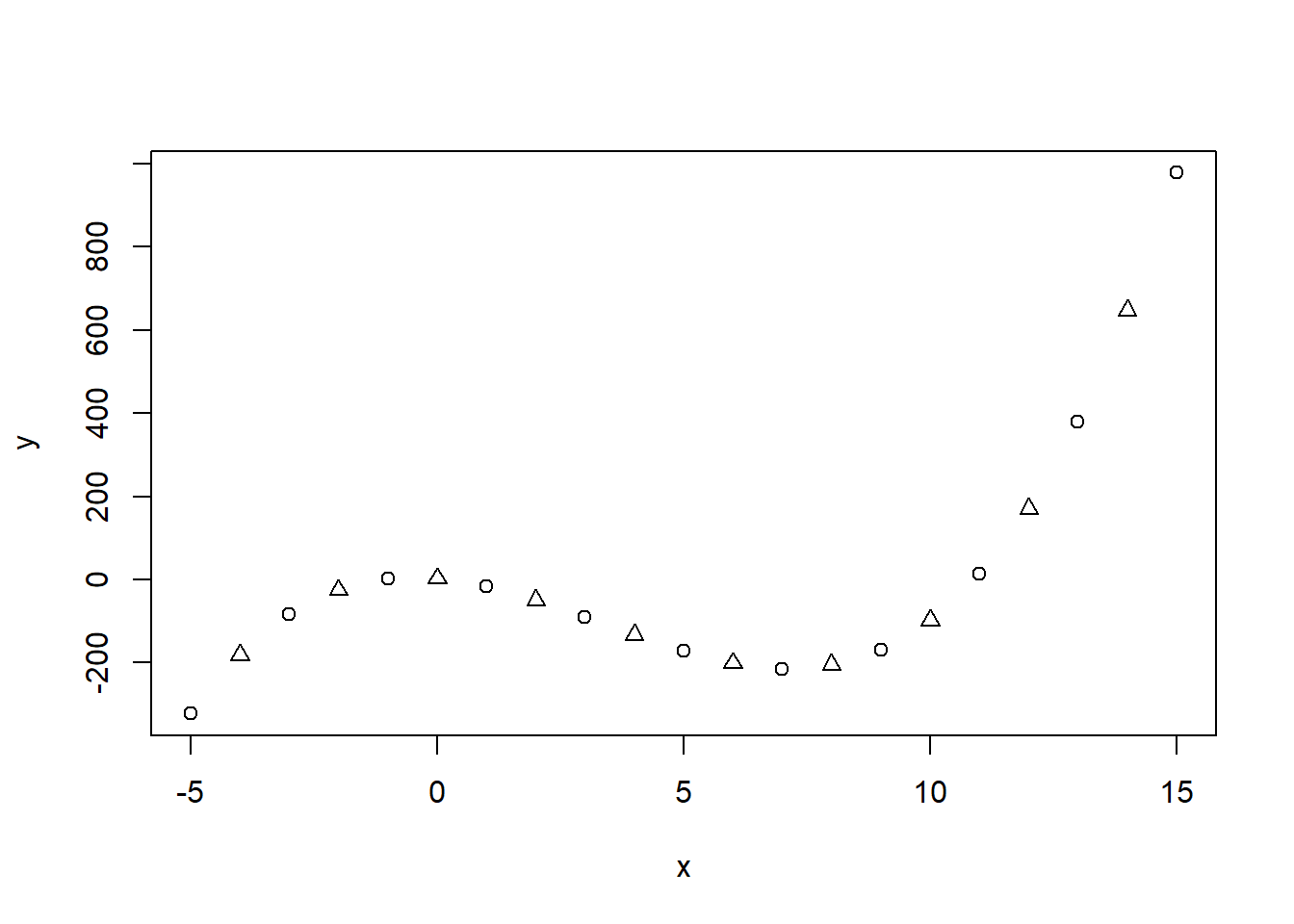

Dar vienas pavyzdys, tik šį kartą kaip taškų simbolius naudosime pirmasias dešimt raidžių

plot(x, y, pch = letters[1:10])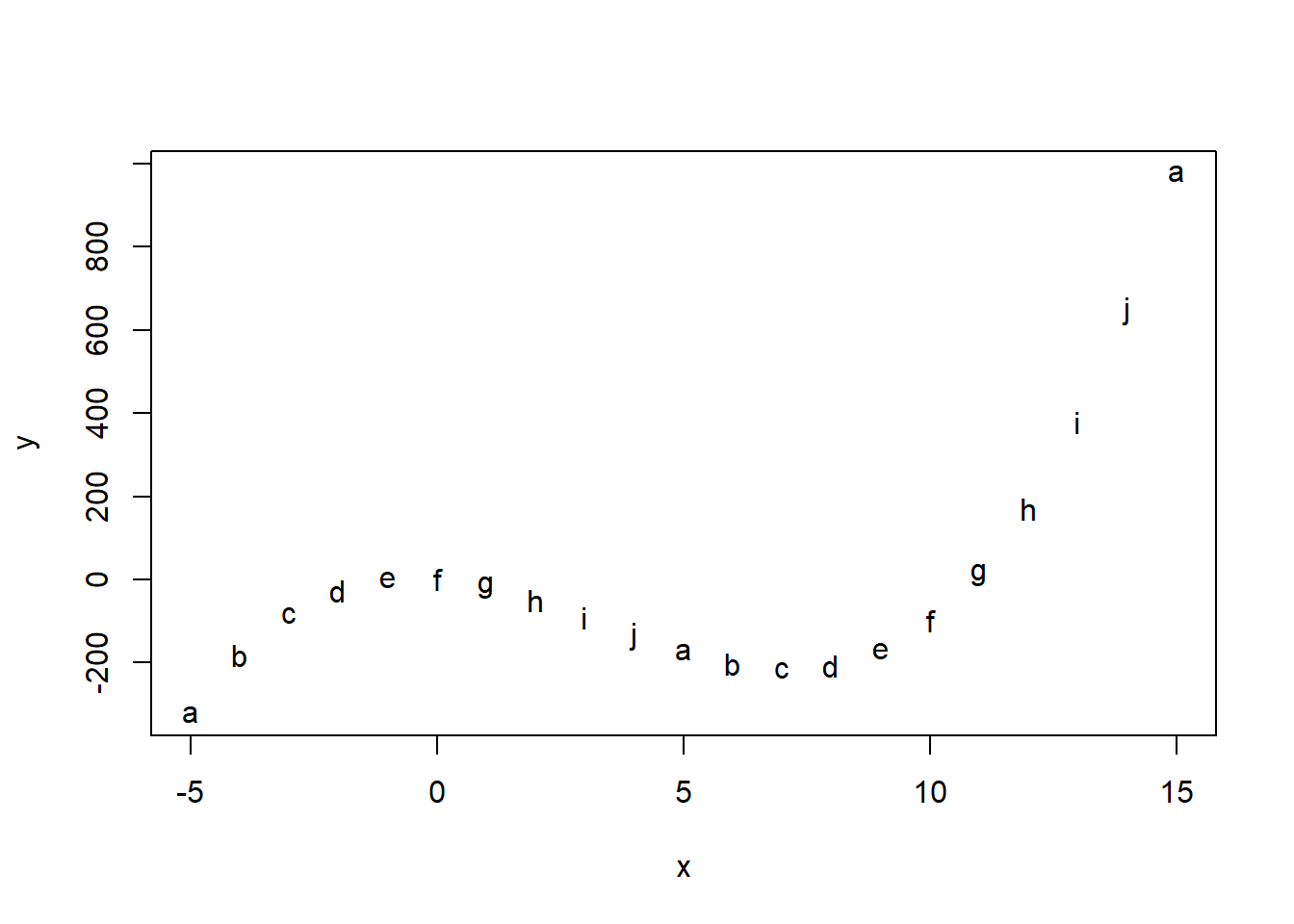

Kelių parametrų reikšmės nurodytos kaip vektoriai.

plot(x, y, pch = 22, cex = 1:3, col = 1:3, bg = 2:4)

Naudojant logines sąlygas galima valdyti spalvas ar simbolius, nes loginės sąlygos rezultatas bus dichotominis vektorius.

plot(x, y, col = factor(y < 0))

Užduotis

Sąlyga

1. Nubraižykite funkcijos \(y = \sin x\) grafiką intervale \([-\pi; \pi]\). Grafike turi būti pavaizduoti:

1. nesujungti taškai \((x, y)\),

2. ištisinė linija be taškų,

3. taškai ir juos jungianti mėlyna punktyrinė linija.

2. Nubraižykite taškų su koordinatėmis \((x, y)\) sklaidos diagramą, kurioje taško simbolio dydis būtų proporcingas koordinatės x reikšmei. Proporcingumo koef. galima pasirinkti laisvai.

3. Nubraižykite tokią taškų su koordinatėmis \((x, y)\) sklaidos diagramą, kurioje ant visus taškus jungiančios kreivės būtų pavaizduoti tik tie taškai, kurių
   koordinatė \(y < 0\).

4. Iš failo data_plot_ex1.csv nuskaitykite duomenų lentelę. Nubraižykite:

   1. šios lentelės kintamųjų \(x\) ir \(y\) sklaidos diagramą,

   2. diagramą, kurioje taškų \((x, y)\) spalva priklauso nuo tos pačios lentelės kintamojo \(z\) reikšmės.

Papildomi funkcijos plot() parametrai

Funkcija plot() turi daug papildomų parametrų, kurie leidžia kontroliuoti grafiko išvaizdą – ašių ribas, pavadinimus, proporcijas ir pan. Pagrindiniai jų:

• main, sub – pagrindinė ir papildoma antraštės,
• xlab, ylab – ašių pavadinimai,
• xlim, ylim – ašių ribos,
• asp – ašių proporcijos (\(y/x\)),
• frame.plot – ar rodyti rėmelį,
• axes, xaxt, yaxt – ar rodyti ašis,
• ann – ar rodyti antraštes.

Žemiau pateikti parametrų naudojimo pavyzdžiai.

plot(x, y, main = "Pagrindinė antraštė", sub = "papildoma antraštė")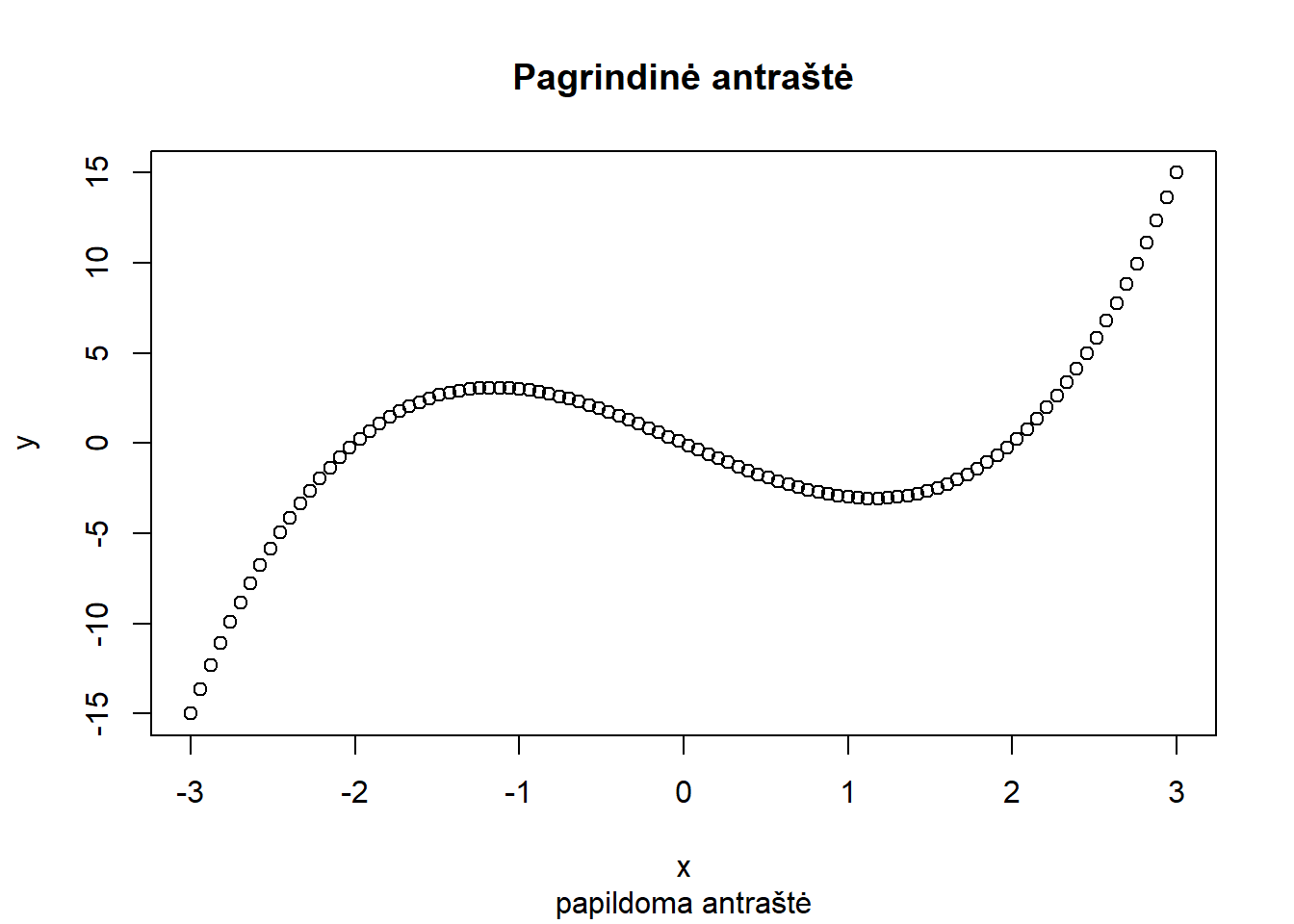

plot(x, y, xlab = "x ašis", ylab = "y ašis")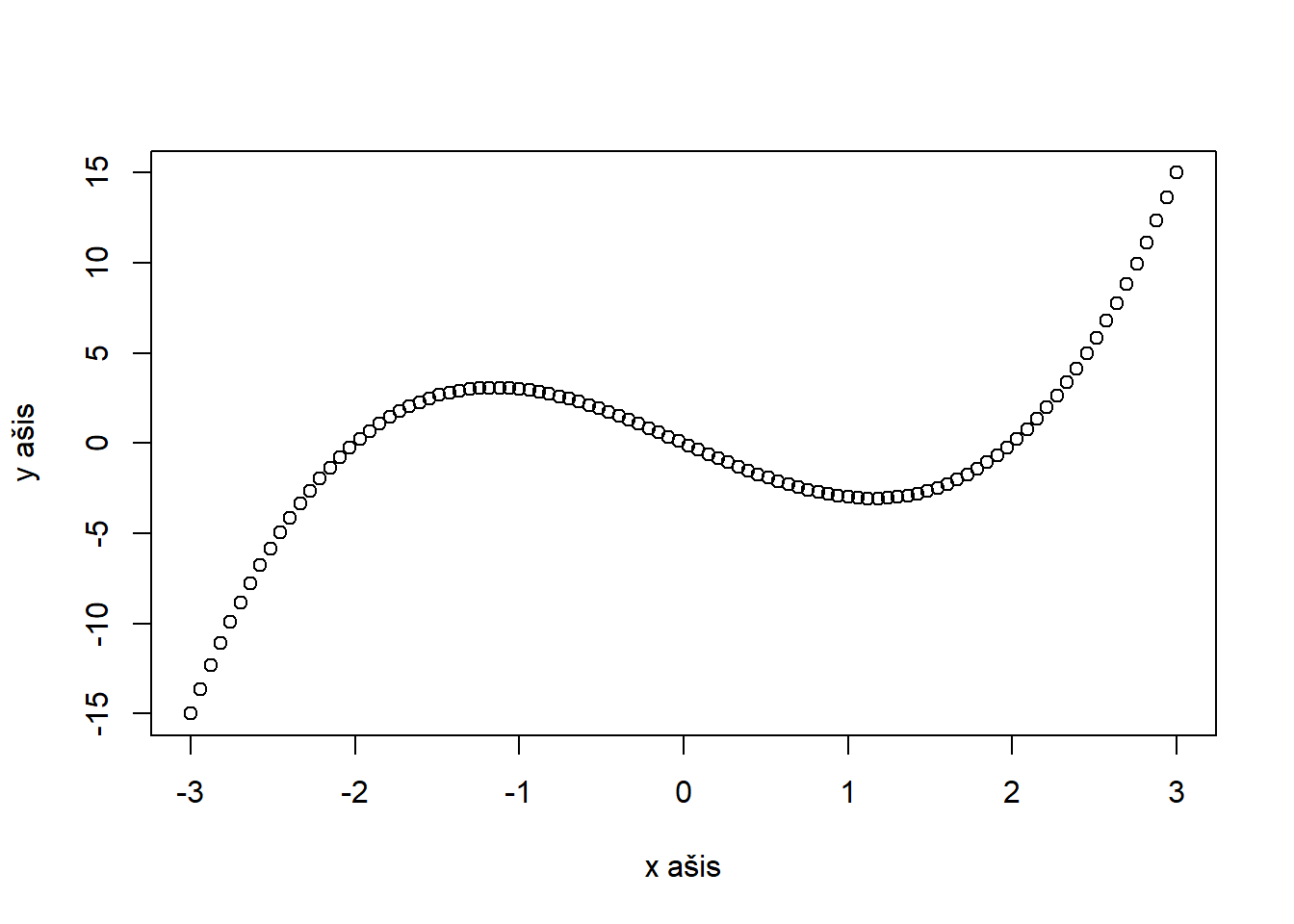

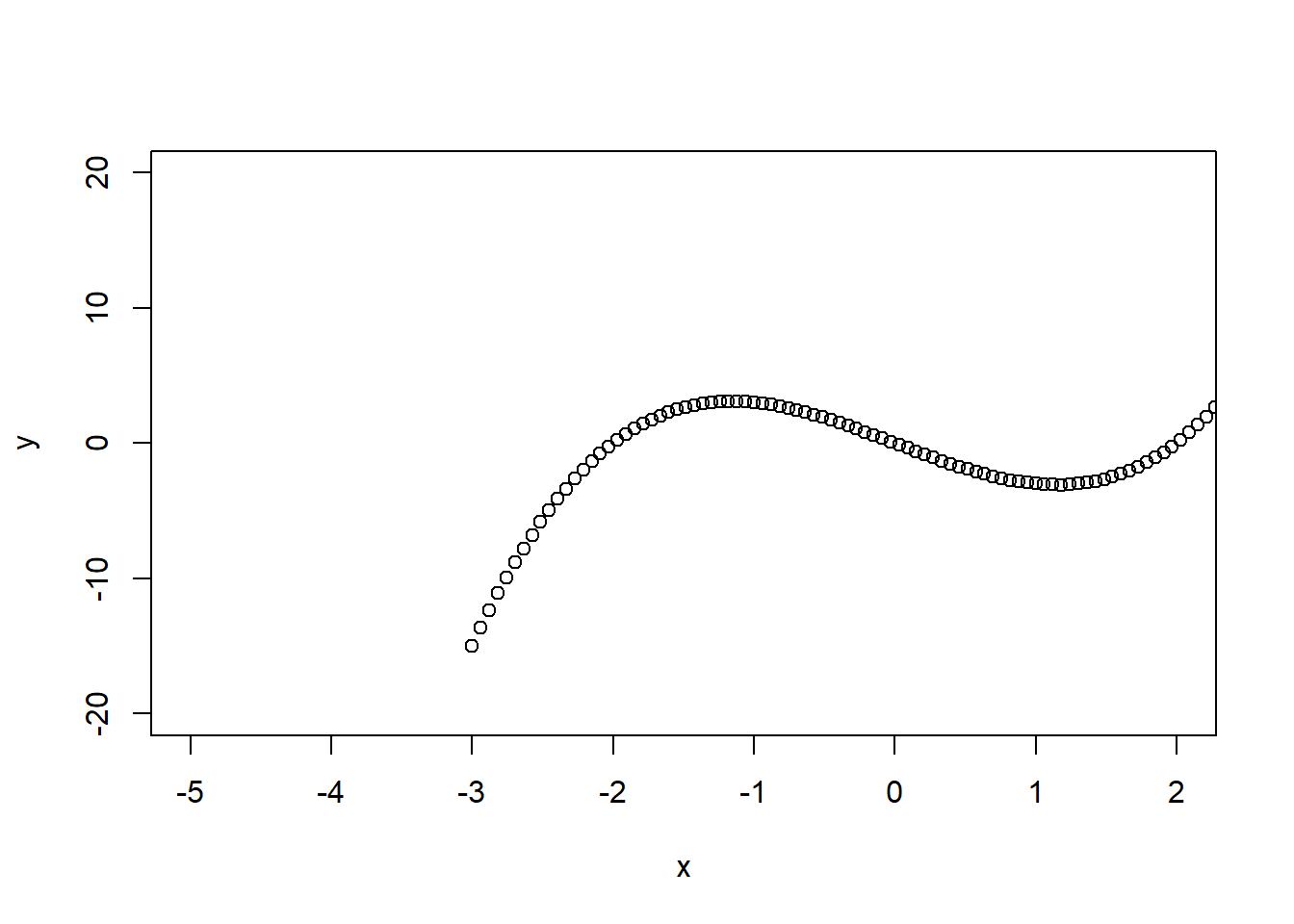
plot(x, y, xlim = c(-5, 2), ylim = c(-20, 20))

plot(x, y, asp = 1/1)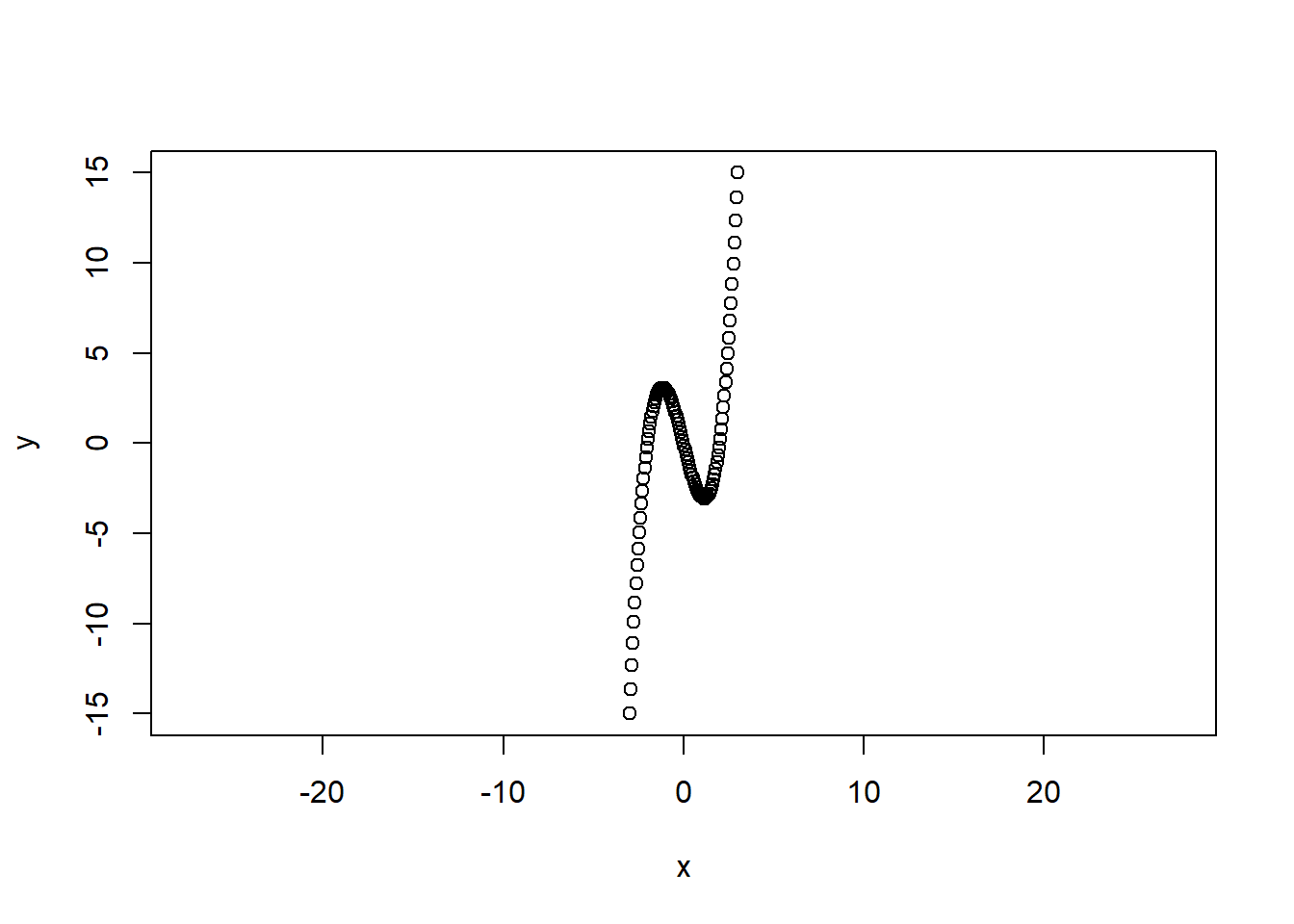

plot(x, y, frame.plot = FALSE)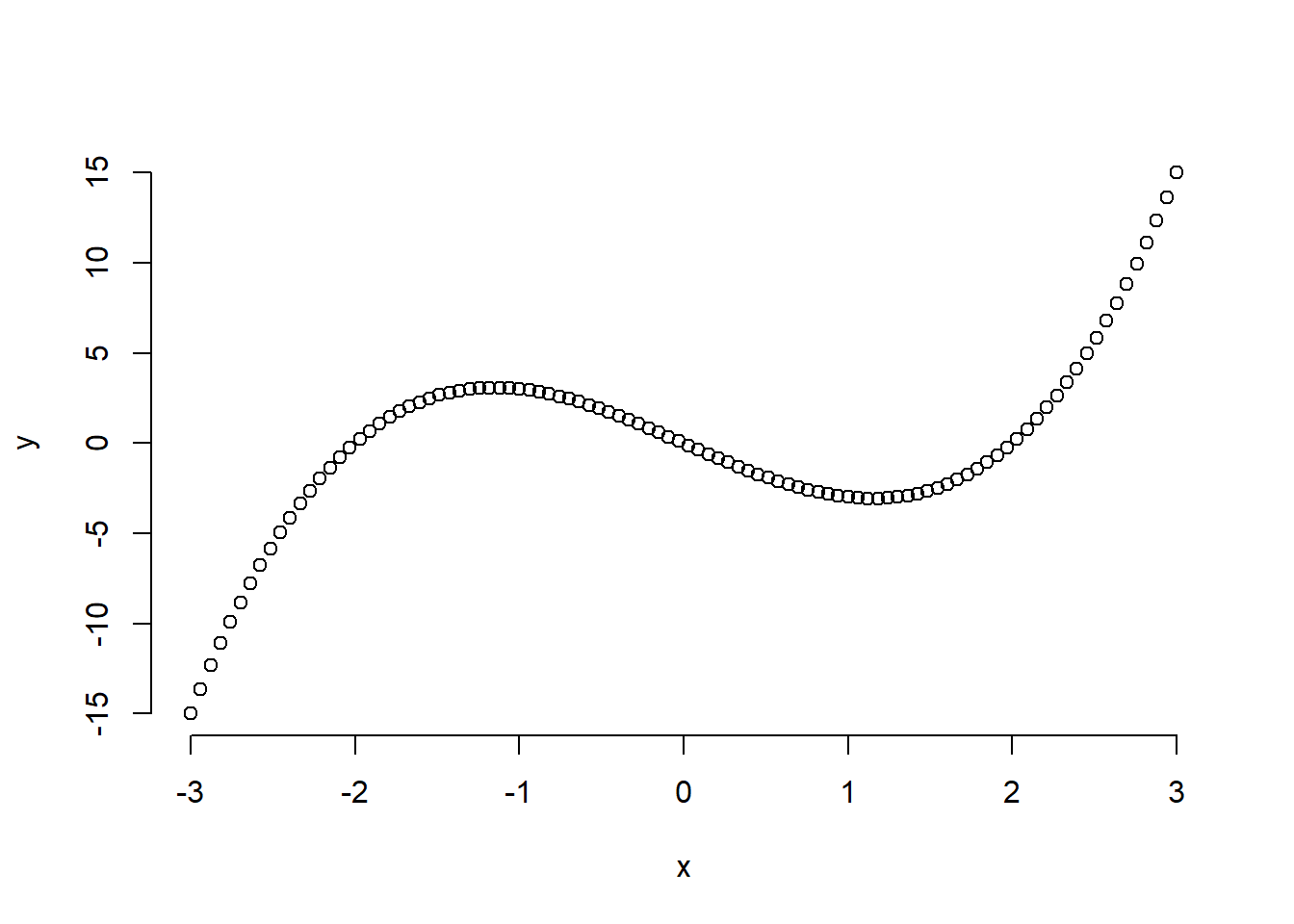

plot(x, y, axes = FALSE)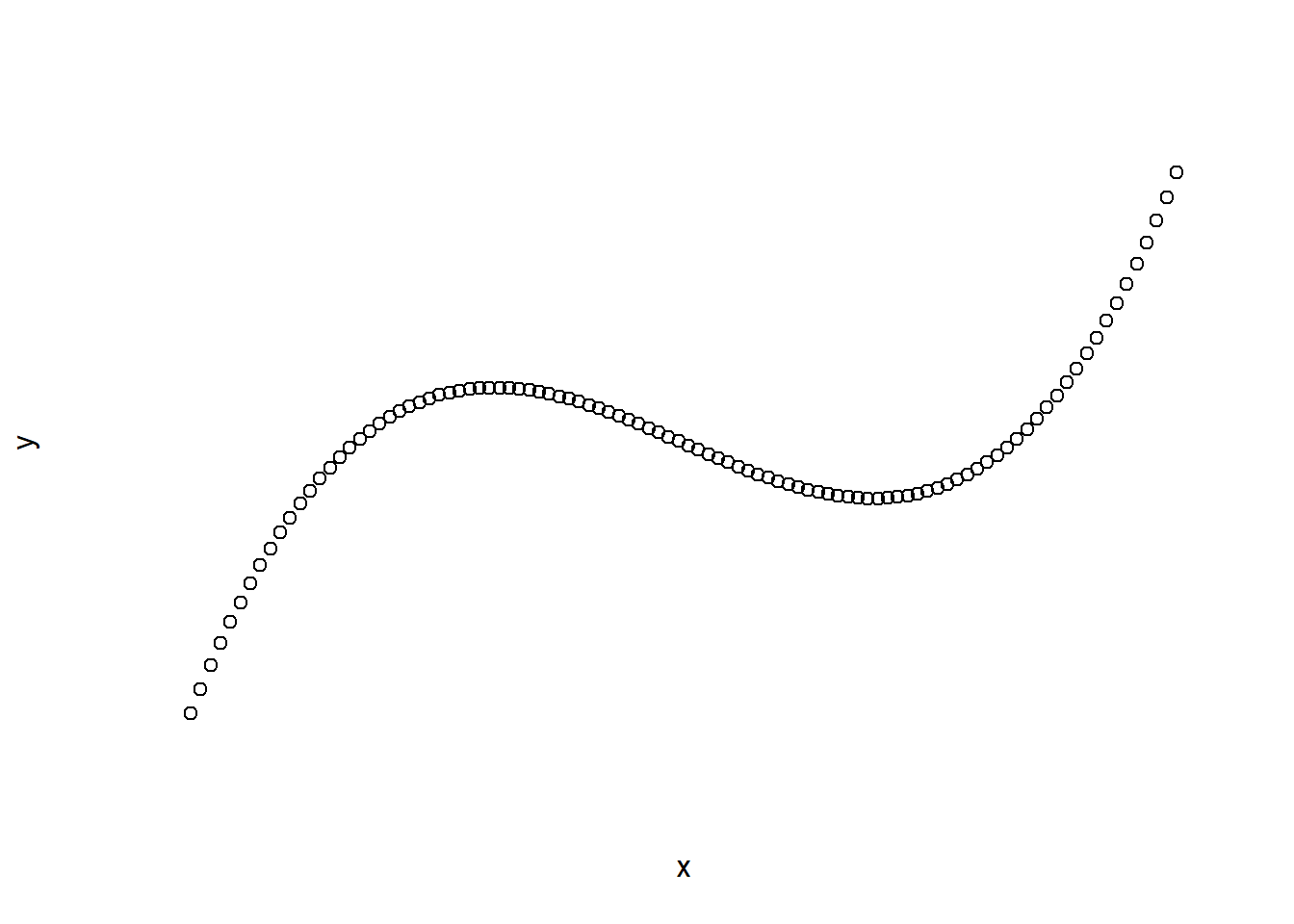

plot(x, y, xaxt = "n")

plot(x, y, ann = FALSE)

Užduotis

Sąlyga

1. Užrašykite komandą, kuri taškų \((x, y)\) sklaidos diagramoje ašies \(Ox\) ribas automatiškai praplėstų: a) po 10 vnt. į abi puses, b) po 10 % į abi puses.

2. Nubraižykite taškų \((x, y)\) sklaidos diagramą, kurioje būtų atvaizduoti tik patys taškai, bet nebūtų nei ašių, nei ašių pavadinimų, nei kitų antraščių.

3. Nubraižykite visus taškus \(10 \times 10\) kvadrate, kurių koordinatės yra natūralieji skaičiai. Grafiko ašių santykis turi būti 1:2, taško simbolis - tuščias kvadratas, abiejų ašių ribos nuo 0 iki 10. Pastaba: naudokite funkciją expand.grid().

4. Nubrėžkite apskritimą su centru taške \((2, 2)\) ir spinduliu \(r = 2\). Naudokite vienodą ašių mastelio santyk. Uždėkite ašių ir pagrindinį grafiko pavadinimus.

8.2 plot() metodai

Kol kas susipažindami su plot() funkcija naudojome tik plot.default() metodą, kuris sukuria dvimačių taškų sklaidos diagramą. Toliau susipažinsime su dar keletą metodų, tokių kaip:

• plot.data.frame – skaitinių duomenų lentelių atvaizdavimui,
• plot.formula – duomenų pagal jų priklausomybės modelį atvaizdavimui,
• plot.function – įvairių funkcijų grafikų bražymui,
• plot.table – dažnių ir kryžminių dažnių lentelių atvaizdavimui,
• plot.factor – kategorinių kintamųjų (faktorių) atvaizdavimui,
• plot.histogram – histogramos braižymui.

Visus funkcijos plot() metodus galima sužinoti naudojant funkciją methods().

methods(plot)
#>  [1] plot.acf*           plot.data.frame*    plot.decomposed.ts*
#>  [4] plot.default        plot.dendrogram*    plot.density*      
#>  [7] plot.ecdf           plot.factor*        plot.formula*      
#> [10] plot.function       plot.hclust*        plot.histogram*    
#> [13] plot.HoltWinters*   plot.isoreg*        plot.lm*           
#> [16] plot.medpolish*     plot.mlm*           plot.ppr*          
#> [19] plot.prcomp*        plot.princomp*      plot.profile*      
#> [22] plot.profile.nls*   plot.raster*        plot.spec*         
#> [25] plot.stepfun        plot.stl*           plot.table*        
#> [28] plot.ts             plot.tskernel*      plot.TukeyHSD*     
#> see '?methods' for accessing help and source code

Metodas sklaidos diagramai pagal formulę vaizdavimui

Dviejų kintamųjų sklaidos diagrama yra vienas iš būdų pastebėti statistinę šių kintamųjų priklausomybę. Ši priklausomybė yra akivaizdi, kai taškų koordinates \((x, y)\) sieja ryšys \(y = f(x)\). Nagrinėjant atsitiktinių dydžių priklausomybę yra rašomas statistinis modelis, kuris R kalboje išreiškiamas per formulę. Kairėje jos pusėje rašomas kintamasis, kuris atitinka koordinatę \(y\), o dešinėje pusėje užrašomas kintamasis \(x\). Funkcija plot(), naudodama metodą plot.formula, pagal šį modelį sudaro dviejų kintamųjų sklaidos diagramą.

modelis <- y ~ x
modelis
#> y ~ x

Pavyzdžiui, sudarysime duomenų lentelės d kintamųjų x ir y sklaidos diagramą. Funkcijai plot() kaip parametrą perduodame kintamųjų sąryšio modelį ir nurodome duomenų lentelę, iš kurios ir paimami modelyje įrašyti kintamieji x ir y.

x <- c(2.0, 1.6, 1.2, 1.0, 1.0, 1.3, 1.6, 2.0, 2.3, 2.8, 2.8, 3.0, 2.8, 2.4, 2.1)
y <- c(0.8, 1.1, 1.3, 1.6, 2.2, 2.5, 2.9, 3.1, 3.0, 2.8, 2.4, 1.8, 1.4, 1.0, 0.9)
z <- c(2.8, 6.1, 4.5, 8.0, 6.7, 9.0, 9.2, 9.3, 7.2, 9.6, 8.6, 8.4, 7.3, 6.1, 3.9)

d <- data.frame(x, y, z)
l <- list(x, y, z)

plot(modelis, data = d)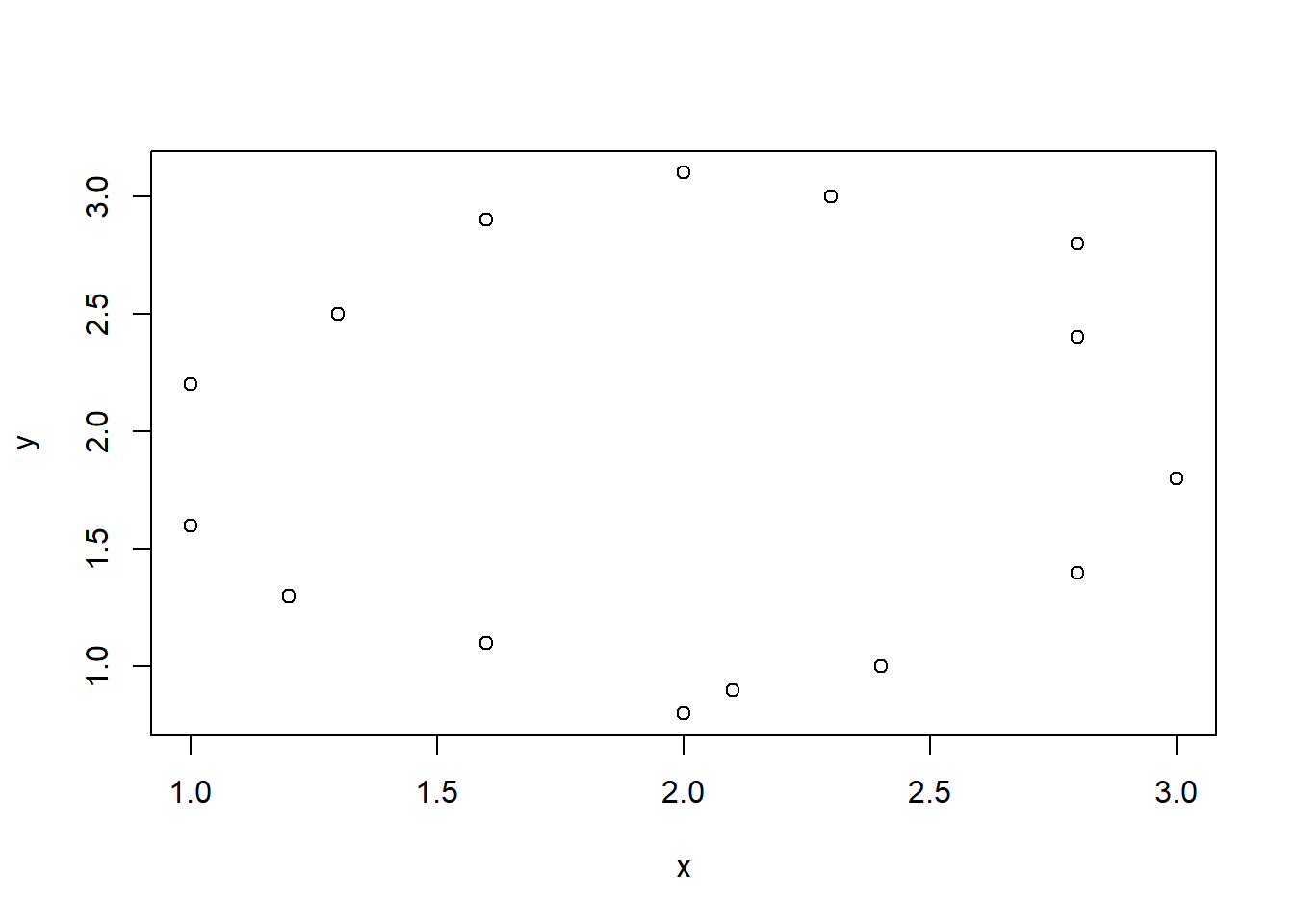

Jeigu modelis, pagal kurį braižoma sklaidos diagrama, nesikeičia, jo išraišką galima įrašyti tiesiai į funkciją plot().

plot(y ~ x, data = d)

Formulėje įrašyti kintamieji nebūtinai turi būti duomenų lentelėje. Pavyzdžiui, nubraižysime sąrašo l kintamųjų x ir y sklaidos diagramą.

plot(y ~ x, data = l)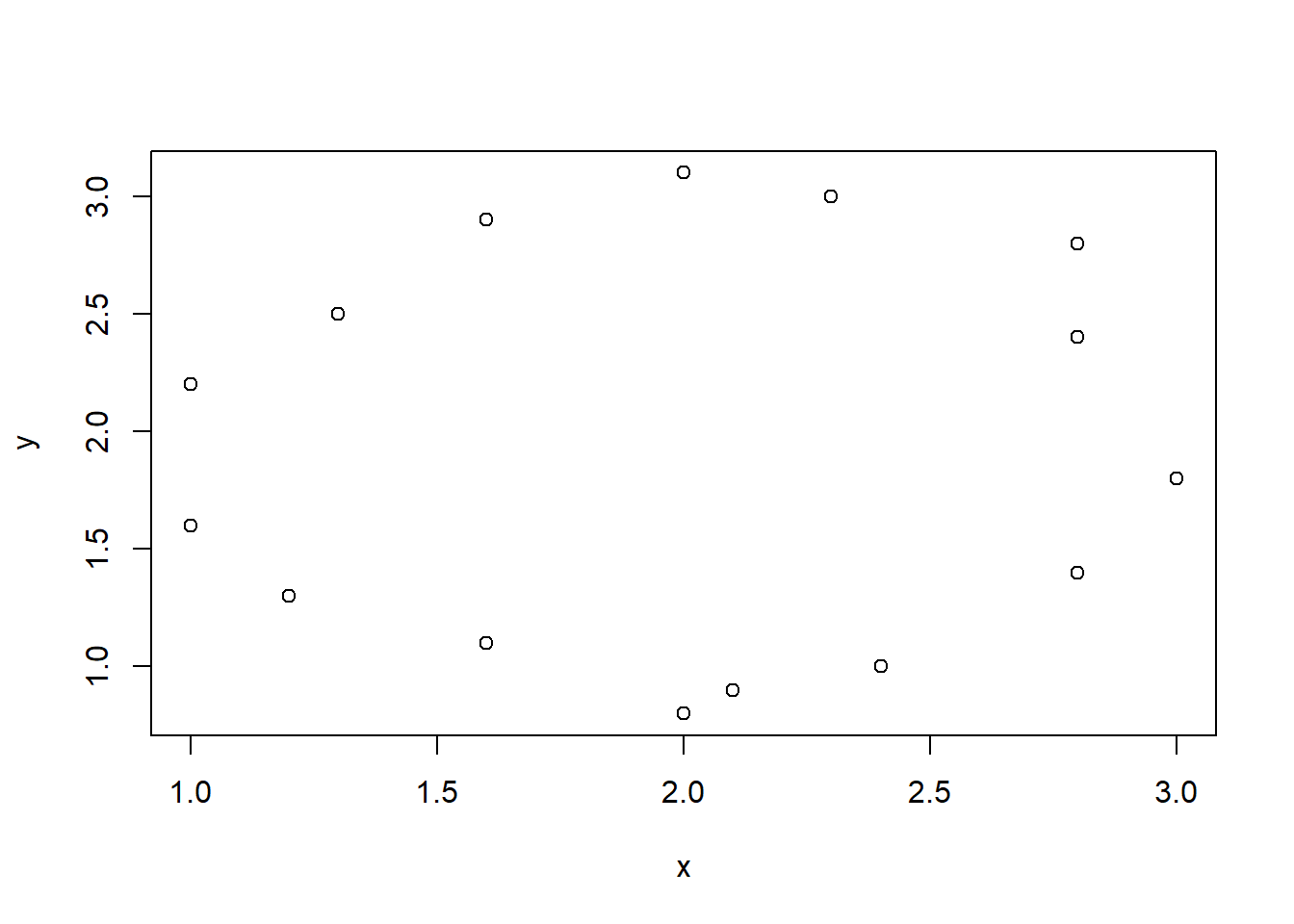

Pastaba. Nenurodžius nei duomenų lentelės, nei sąrašo pavadinimo, bus braižoma tokius pat pavadinimus turinčių kintamųjų (jei tokie yra) sklaidos diagrama.

Naudojant modelį, galima užrašyti labai įvairias tų pačių kintamųjų tarpusavio priklausomybes. Užrašysime keletą dažniausiai pasitaikančių modelių:

• y ~ x – taškų su koordinatėmis \((x, y)\) sklaidos diagrama,
• y ~ 1 – taškų \((i, y_i)\) diagrama, kai \(i\) – \(y\) elementų eilės numeris,
• ~ x – taškų su koordinatėmis \((x, 1)\) išsidėstymo tiesėje diagrama,
• ~ x + y – ta pati taškų \((x, y)\) sklaidos diagrama,
• ~ x + y + z – trijų kintamųjų \(x\), \(y\) ir \(z\) porų sklaidos diagramos.

Naudodami duomenų lentelės d kintamuosius, pagal šiuos modelius nubraižysime visas šias sklaidos diagramas.

plot(y ~ x, data = d)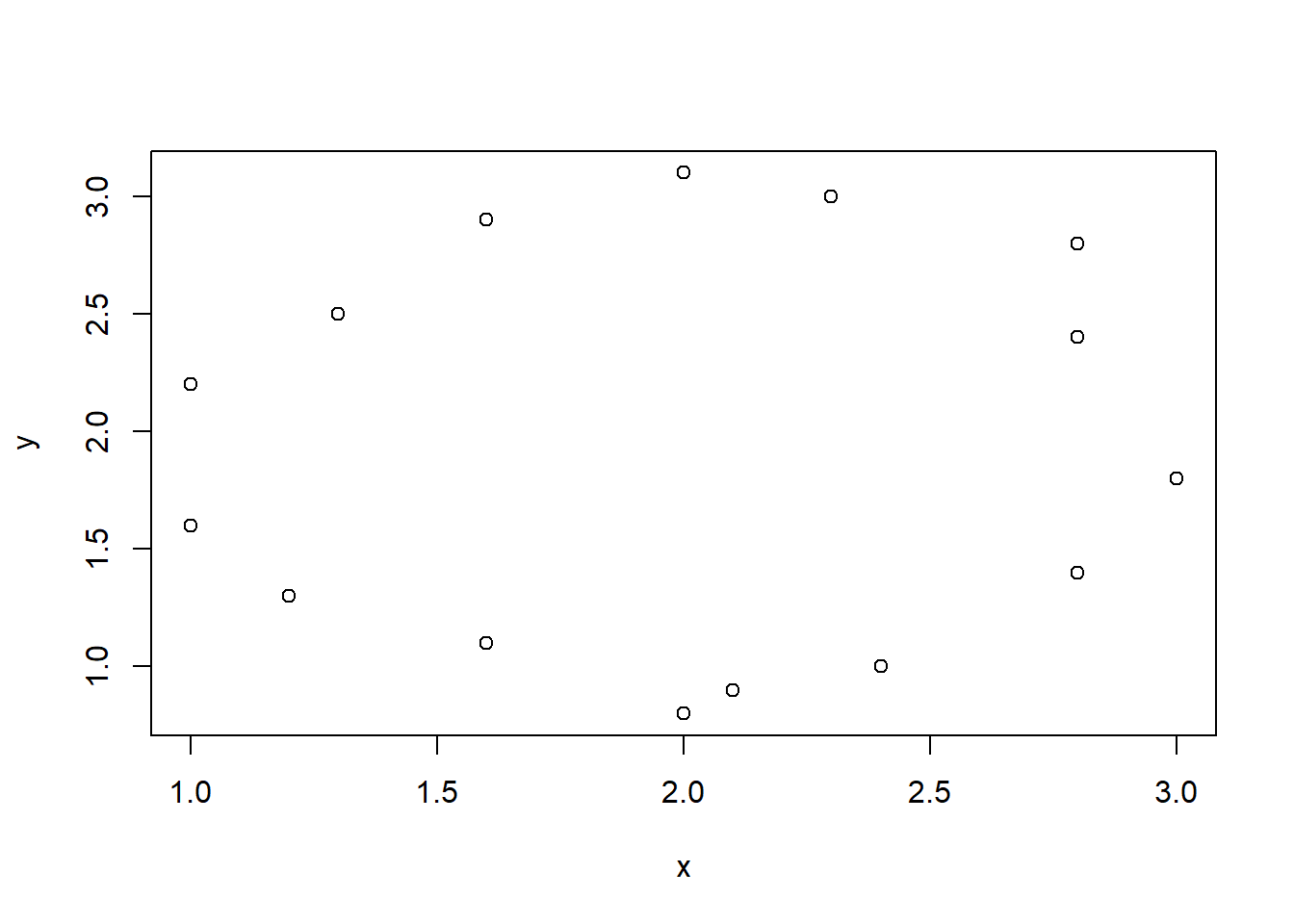

plot(x ~ 1, data = d)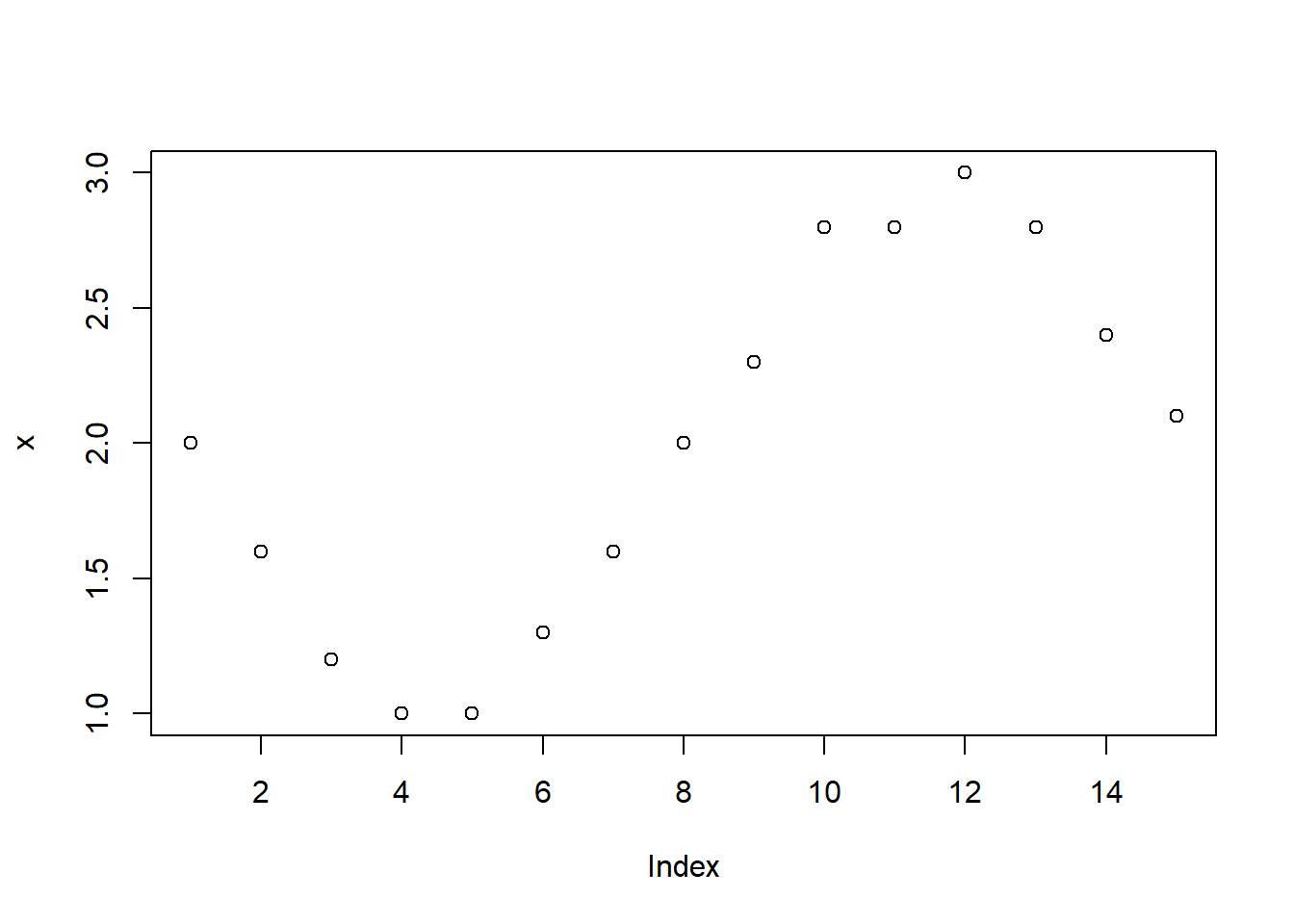

plot(y ~ 1, data = d)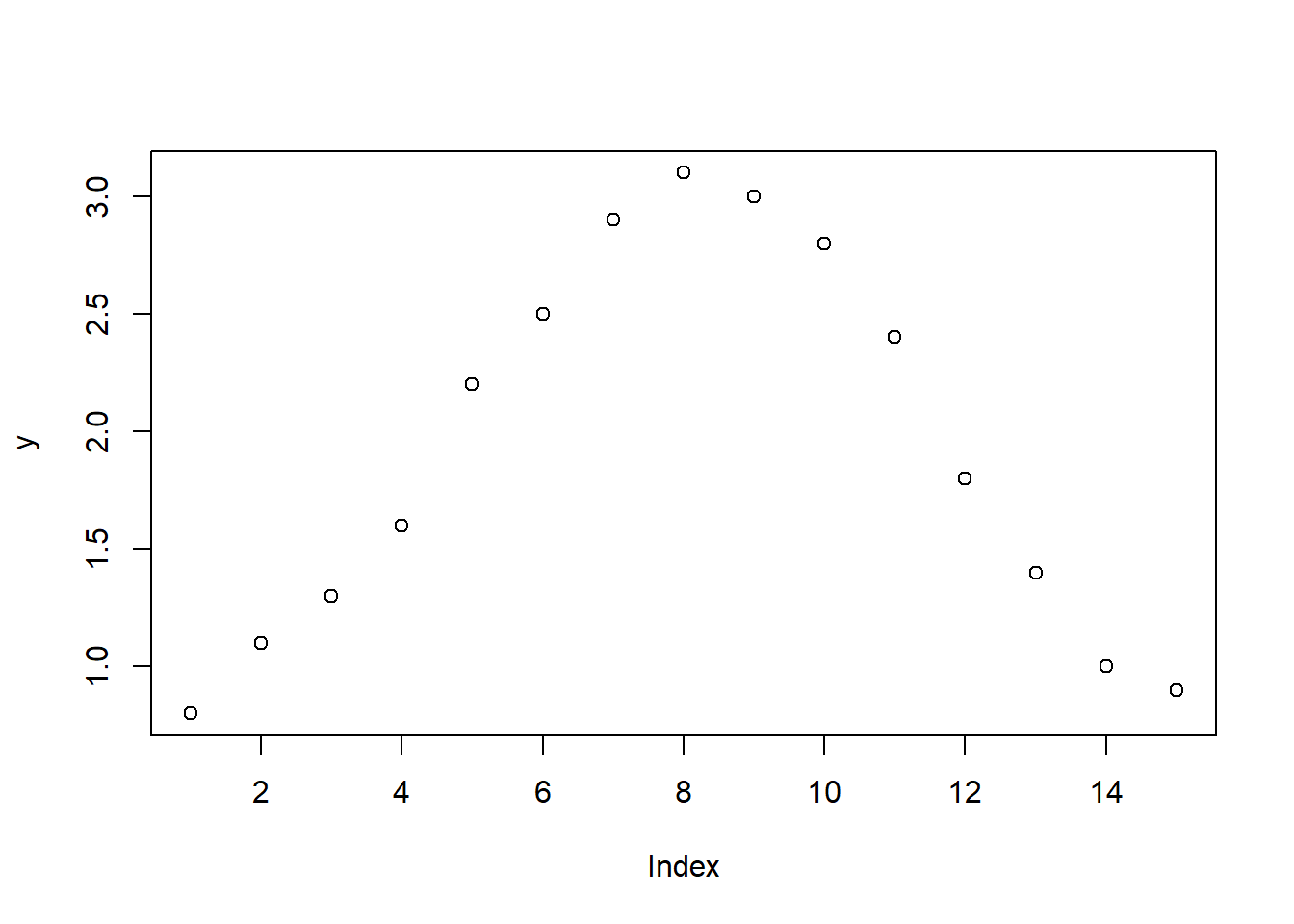

plot( ~ x, data = d)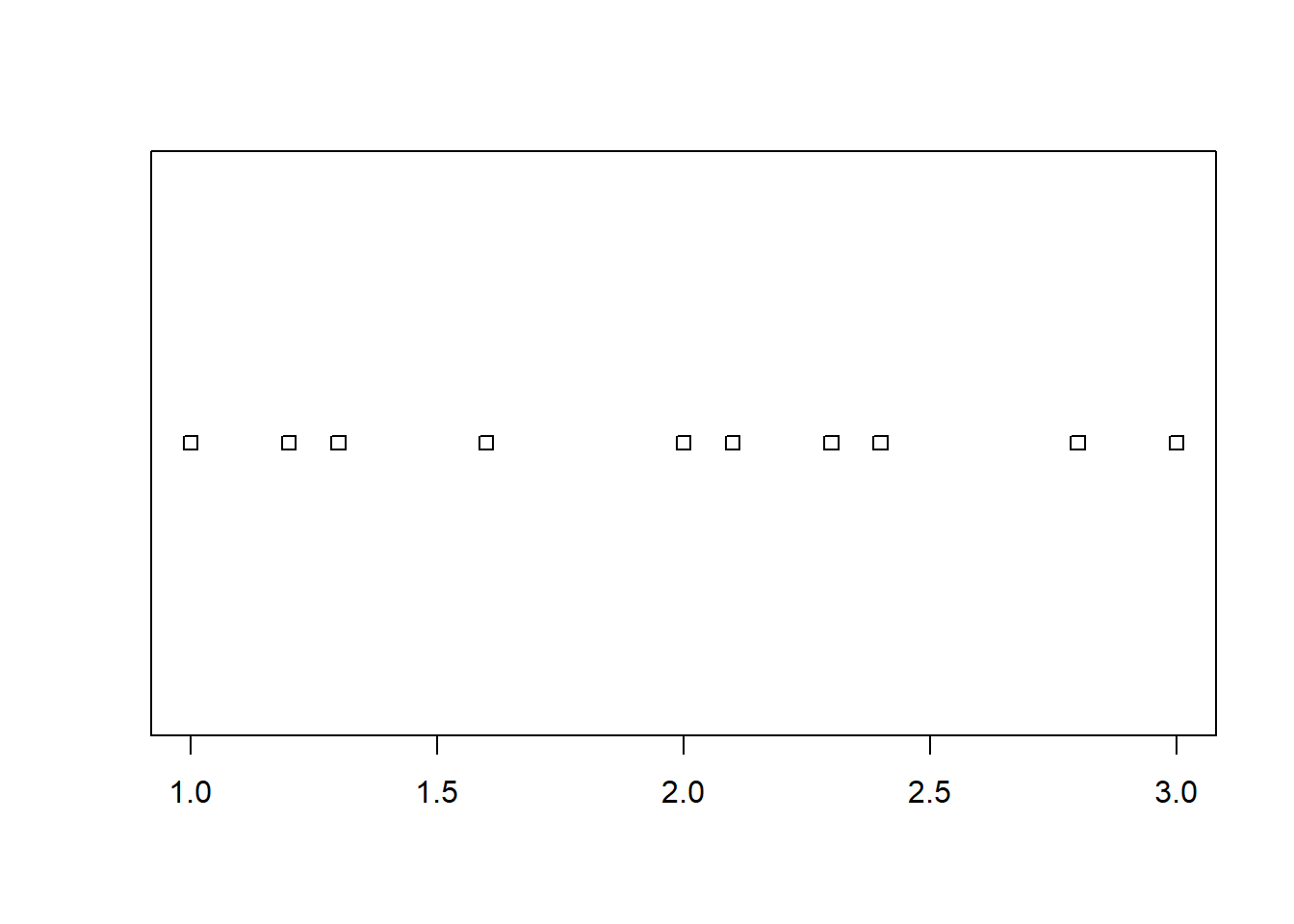

plot( ~ y, data = d)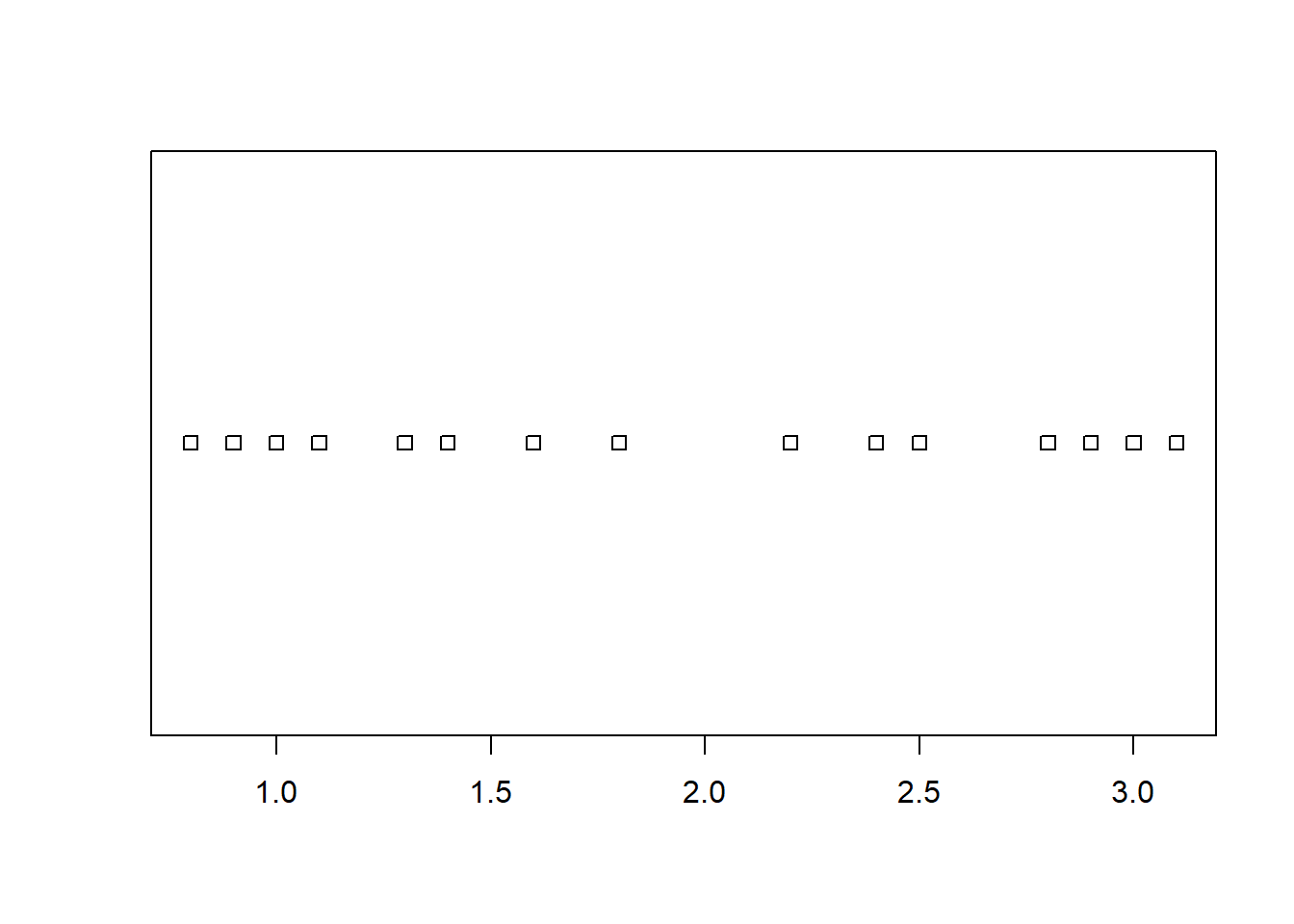

plot( ~ z, data = d)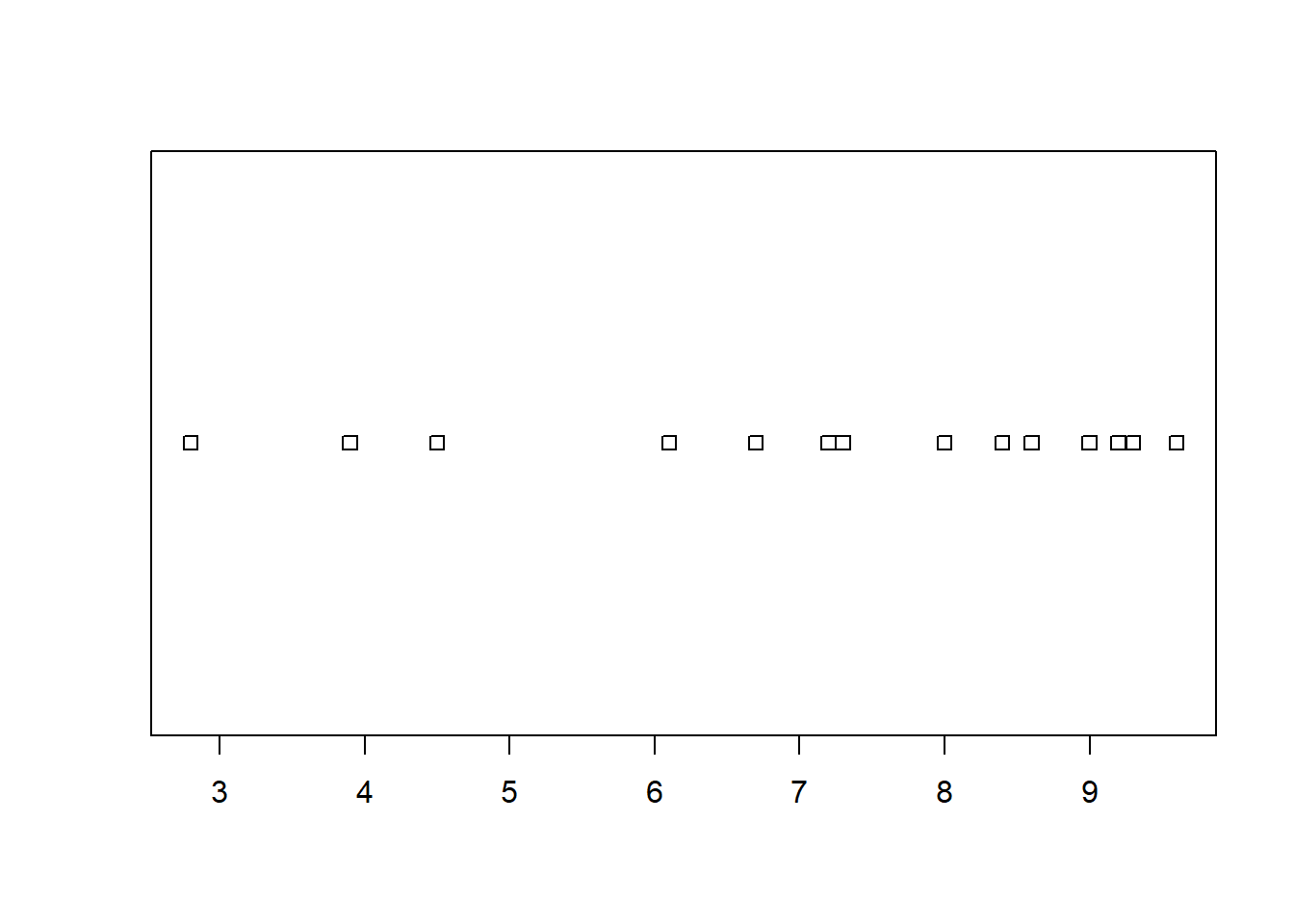

plot( ~ x + y,     data = d)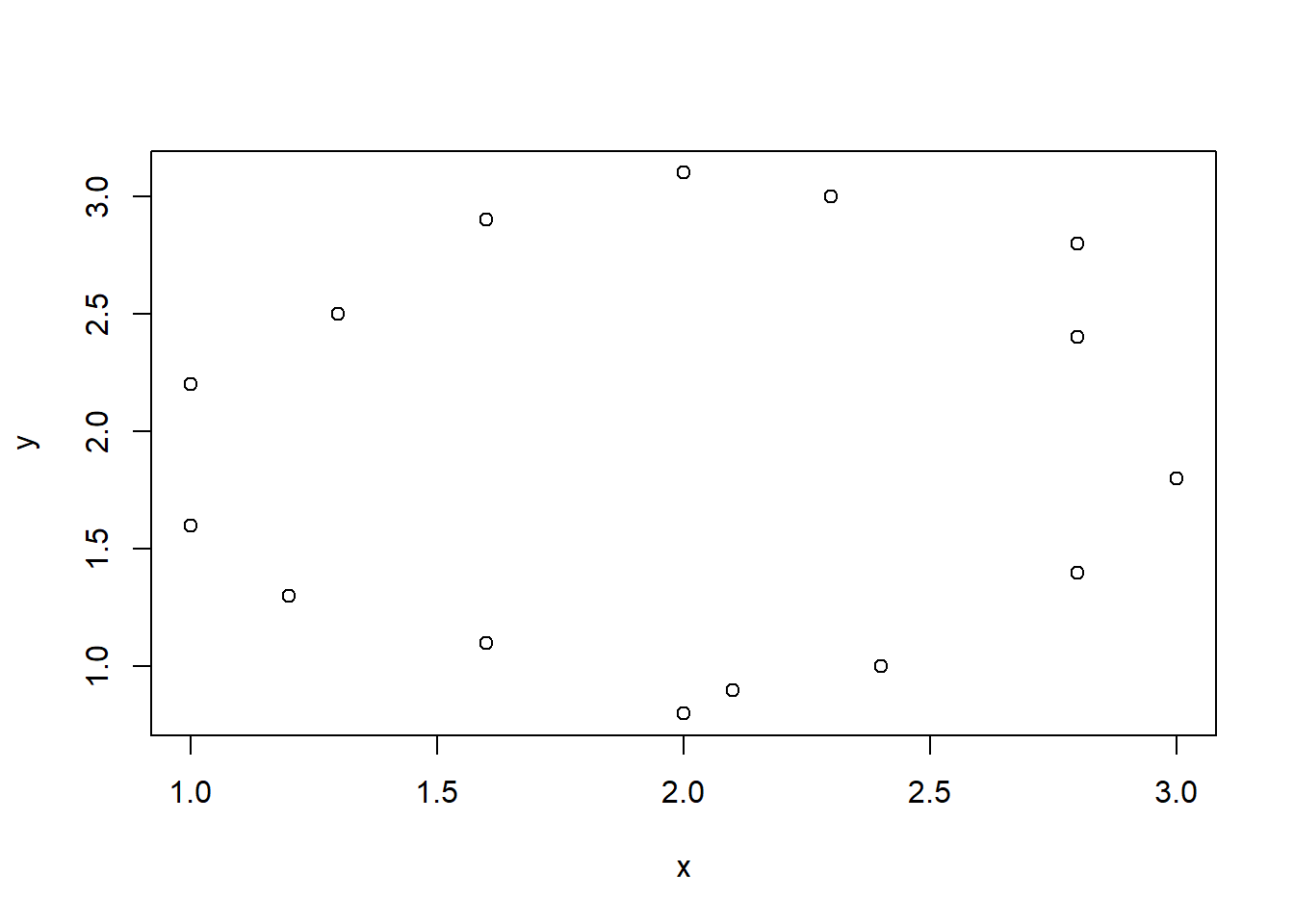

plot( ~ x + y + z, data = d)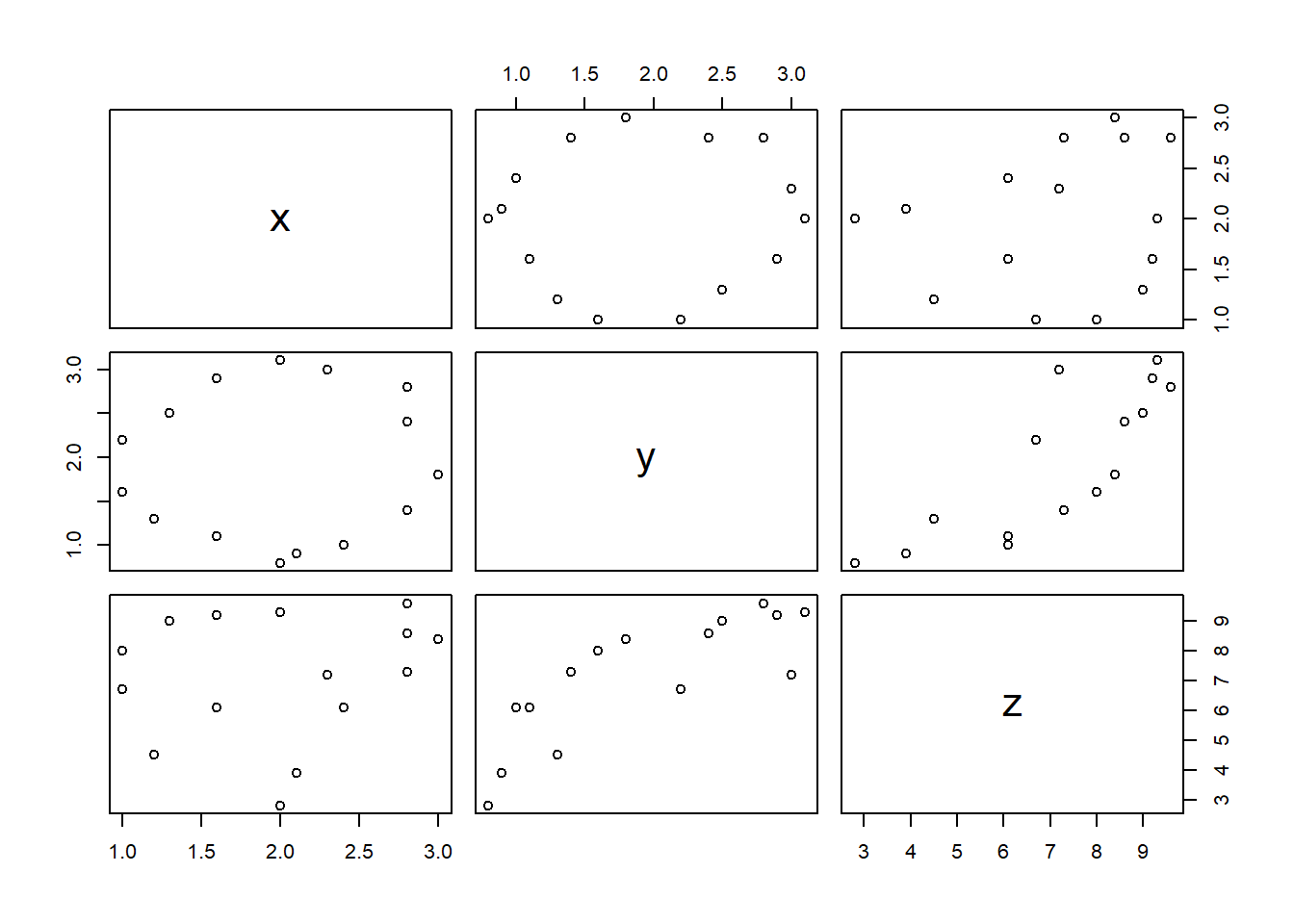

Užduotis

Sąlyga

1. Nubraižykite elipsės su centru koordinačių pradžioje grafiką. Tegul ilgoji elipsės pusašė lygi 5, o trumpoji – 3.

2. Apskaičiuokite Archimedo spiralės 1000 taškų koordinates, nubraižykite jos grafiką. Braižant grafiką, reikia nurodyti fiksuotą 1:1 kraštinių santykį.

3. Lentelėje cars yra automobilio greičio ir stabdymo kelio matavimų duomenys. Sudarykite stabdymo kelio ir automobilio greičio tarpusavio priklausomybės modelį ir nubraižykite jį atitinkantį kintamųjų sklaidos diagramą.

Metodas funkcijos grafiko braižymui

Dar vienas funkcijos plot() metodas yra funkcijų \(y = f(x)\) braižymas. Naudojant šį metodą, funkcijos parametrai yra šie:

Argumentas	Reikšmė
x	funkcijos \(f(x)\) pavadinimas arba jos išraiška
from	funkcijos braižymo intervalo pradžia
to	funkcijos braižymo intervalo pabaiga
n	taškų skaičius intervale [from, to]

Pavyzdžiui sudarysime racionaliosios trupmenos \(y = P(x)/Q(x)\), \(P(x), Q(x)\) dvi racionaliosios funkcijos, grafiką. Jeigu nenurodomos intervalo pradžios ir pabaigos reikšmės, grafikas braižomas intervale \([0, 1]\).

f.x <- function(x){
  y <- x/(x^2 + x + 1)
  return(y)
}

plot(f.x)

plot(f.x, from = -5, to = 5)

Kadangi funkcijoje f.x atliekamas tik vienas veiksmas, tai kompaktiškiau atrodo (vienam kartui) braižomos funkcijos \(f(x)\) užrašymas pačioje plot() funkcijoje.

plot(function(x)  x/(x^2 + x + 1), -5, 5)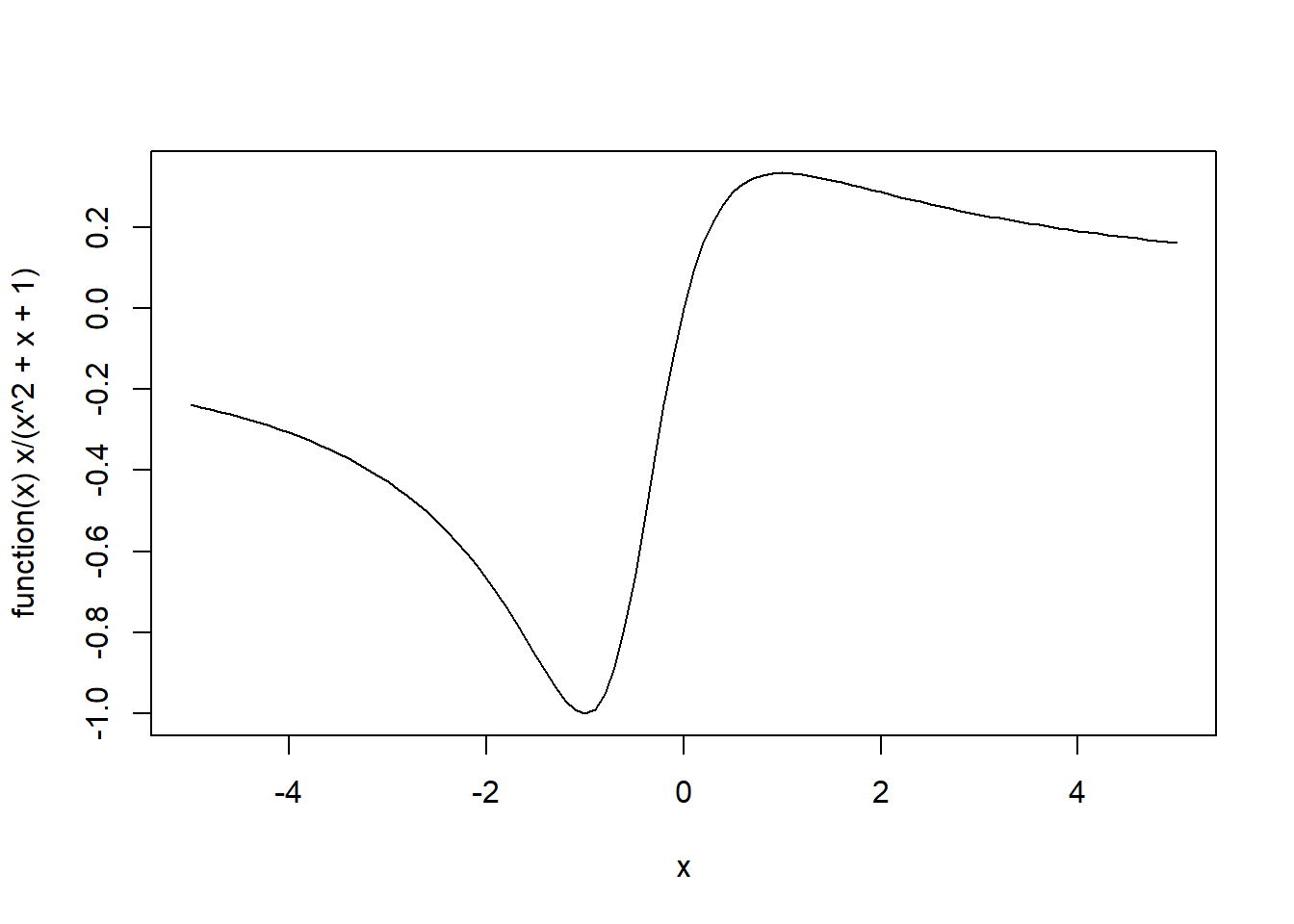

Grafikų braižymo funkcijos ne visada atlieka tik būtent braižymo paskirtį. Jos kaip ir kitos funkcijos gali grąžinti tam tikrą objektą. Metodo plot.function() grąžinamas objektas yra koordinačių \(x\) ir \(y\) sąrašas.

xy.sarasas <- plot(f.x, -5, 5)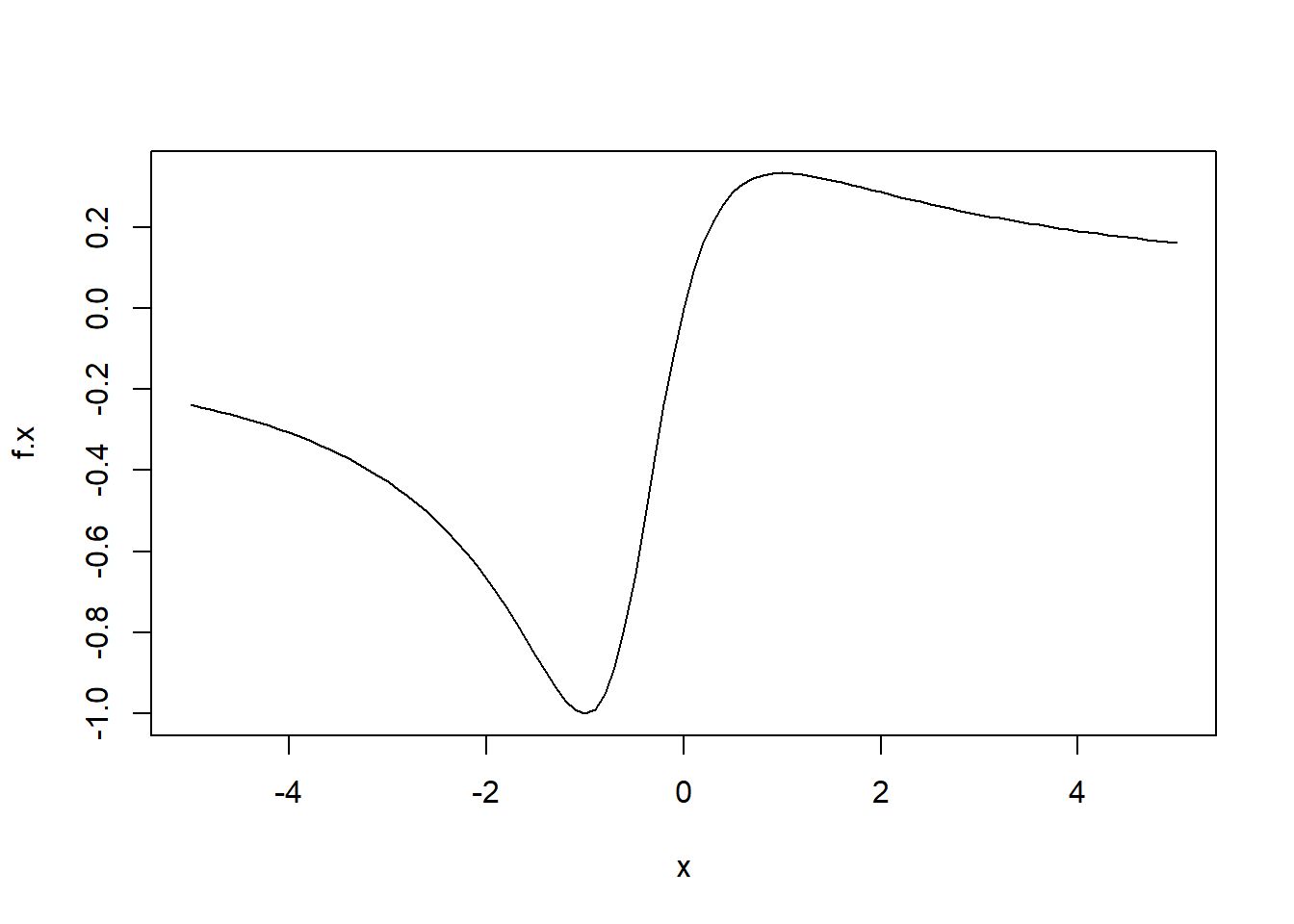

xy.sarasas
#> $x
#>   [1] -5.0 -4.9 -4.8 -4.7 -4.6 -4.5 -4.4 -4.3 -4.2 -4.1 -4.0 -3.9 -3.8 -3.7 -3.6
#>  [16] -3.5 -3.4 -3.3 -3.2 -3.1 -3.0 -2.9 -2.8 -2.7 -2.6 -2.5 -2.4 -2.3 -2.2 -2.1
#>  [31] -2.0 -1.9 -1.8 -1.7 -1.6 -1.5 -1.4 -1.3 -1.2 -1.1 -1.0 -0.9 -0.8 -0.7 -0.6
#>  [46] -0.5 -0.4 -0.3 -0.2 -0.1  0.0  0.1  0.2  0.3  0.4  0.5  0.6  0.7  0.8  0.9
#>  [61]  1.0  1.1  1.2  1.3  1.4  1.5  1.6  1.7  1.8  1.9  2.0  2.1  2.2  2.3  2.4
#>  [76]  2.5  2.6  2.7  2.8  2.9  3.0  3.1  3.2  3.3  3.4  3.5  3.6  3.7  3.8  3.9
#>  [91]  4.0  4.1  4.2  4.3  4.4  4.5  4.6  4.7  4.8  4.9  5.0
#> 
#> $y
#>   [1] -0.23809524 -0.24365987 -0.24948025 -0.25557368 -0.26195900 -0.26865672
#>   [7] -0.27568922 -0.28308097 -0.29085873 -0.29905179 -0.30769231 -0.31681560
#>  [13] -0.32646048 -0.33666970 -0.34749035 -0.35897436 -0.37117904 -0.38416764
#>  [19] -0.39800995 -0.41278296 -0.42857143 -0.44546851 -0.46357616 -0.48300537
#>  [25] -0.50387597 -0.52631579 -0.55045872 -0.57644110 -0.60439560 -0.63444109
#>  [31] -0.66666667 -0.70110701 -0.73770492 -0.77625571 -0.81632653 -0.85714286
#>  [37] -0.89743590 -0.93525180 -0.96774194 -0.99099099 -1.00000000 -0.98901099
#>  [43] -0.95238095 -0.88607595 -0.78947368 -0.66666667 -0.52631579 -0.37974684
#>  [49] -0.23809524 -0.10989011  0.00000000  0.09009009  0.16129032  0.21582734
#>  [55]  0.25641026  0.28571429  0.30612245  0.31963470  0.32786885  0.33210332
#>  [61]  0.33333333  0.33232628  0.32967033  0.32581454  0.32110092  0.31578947
#>  [67]  0.31007752  0.30411449  0.29801325  0.29185868  0.28571429  0.27962716
#>  [73]  0.27363184  0.26775320  0.26200873  0.25641026  0.25096525  0.24567789
#>  [79]  0.24054983  0.23558083  0.23076923  0.22611233  0.22160665  0.21724819
#>  [85]  0.21303258  0.20895522  0.20501139  0.20119630  0.19750520  0.19393337
#>  [91]  0.19047619  0.18712916  0.18388792  0.18074821  0.17770598  0.17475728
#>  [97]  0.17189836  0.16912558  0.16643551  0.16382481  0.16129032

plot(xy.sarasas)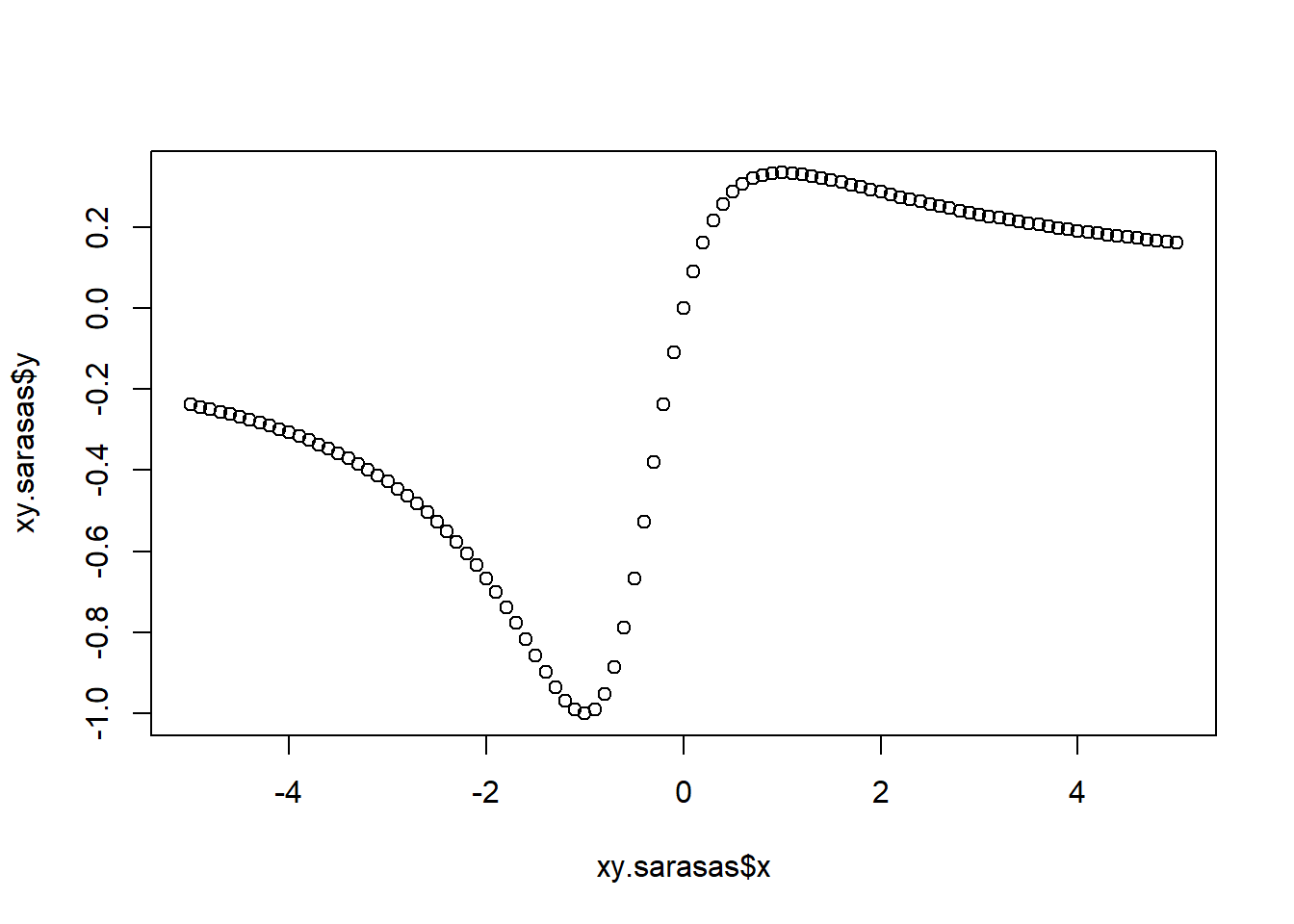

R turi daug praktikoje reikalingų ir dažnai taikomų funkcijų, kurių atskirai užrašyti nereikia – pakanka žinoti jų pavadinimus. Pavyzdžiui, atvaizduosime funkcijos \(y = \sin x\) grafiką intervale \([0, \pi]\).

plot(sin, 0, pi)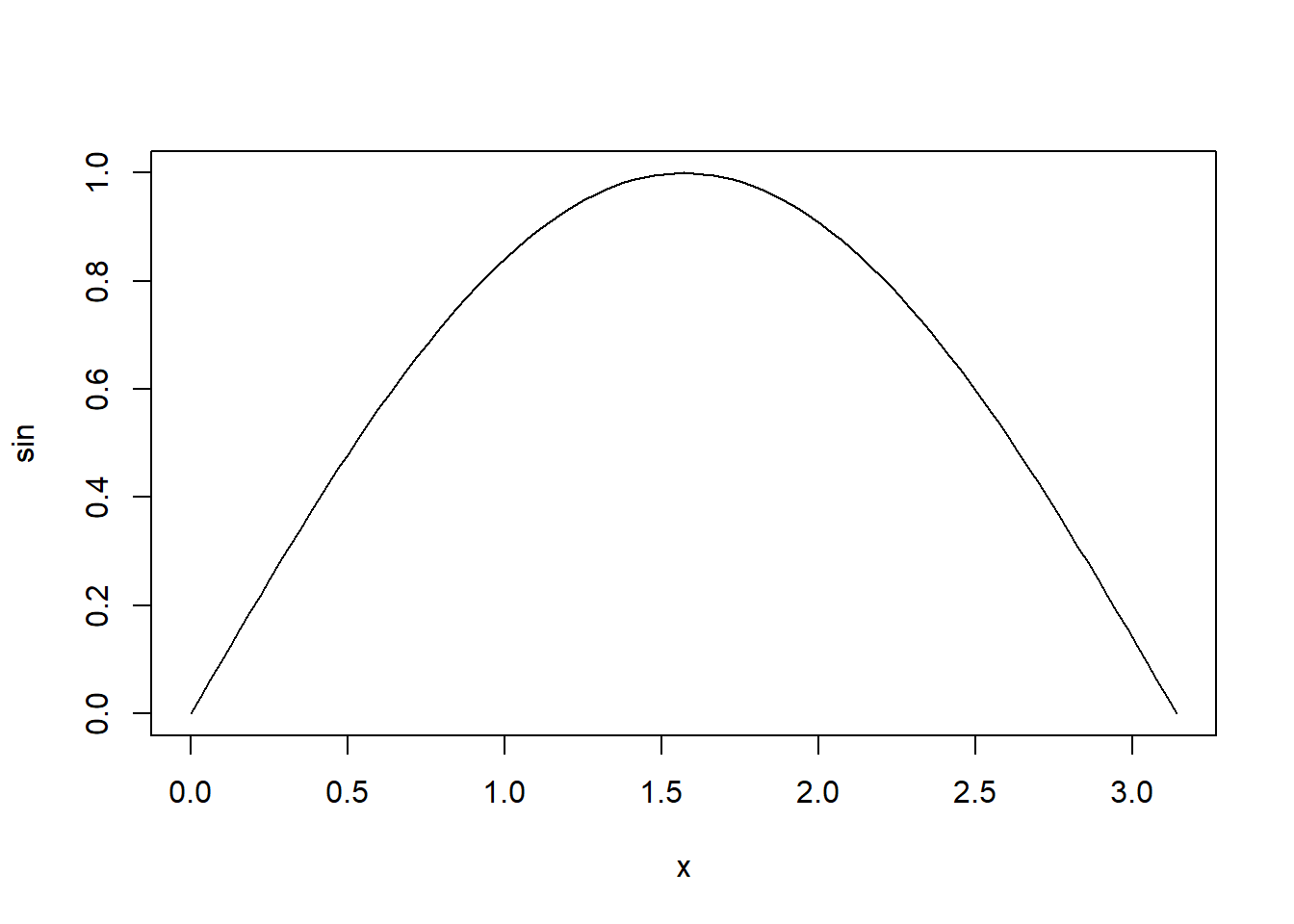

Užduotis

Sąlyga

1. Panaudojant standartinę R funkciją, nubraižykite funkcijos \(y = |x|\) grafiką intervale \([-1, 1]\).

2. Naudodami standartines trigonometrines R funkcijas, nubraižykite funkcijos \(y = \arcsin(\sin x)\) grafiką intervale \([-2\pi, 2\pi]\).

Metodai dažnių lentelėms ir faktoriams

!!! PASTABA: įtraukti prieš tai skyrelį apie dažnių lenteles !!!

Funkcija plot() taip pat gali atvaizduoti dažnių lenteles. Vieno kintamojo dažnių lentelė atvaizduojama kaip stulpelinė diagrama, kur kintamojo reikšmę atitinkančio stulpelio aukštis lygus tos reikšmės dažniui - pasikartojimų skaičiui.

Pavyzdžiui, sudarysime dažnių lentelę iš raidžių sudaryto vektoriaus elementams ir atvaizduosimę šią lentelę.

g <- c("A", "B", "D", "A", "C", "C", "C", "C", "C", "C", "A", "A", "D", "B", "B")

t <- table(g)
t
#> g
#> A B C D 
#> 4 3 6 2

plot(t)

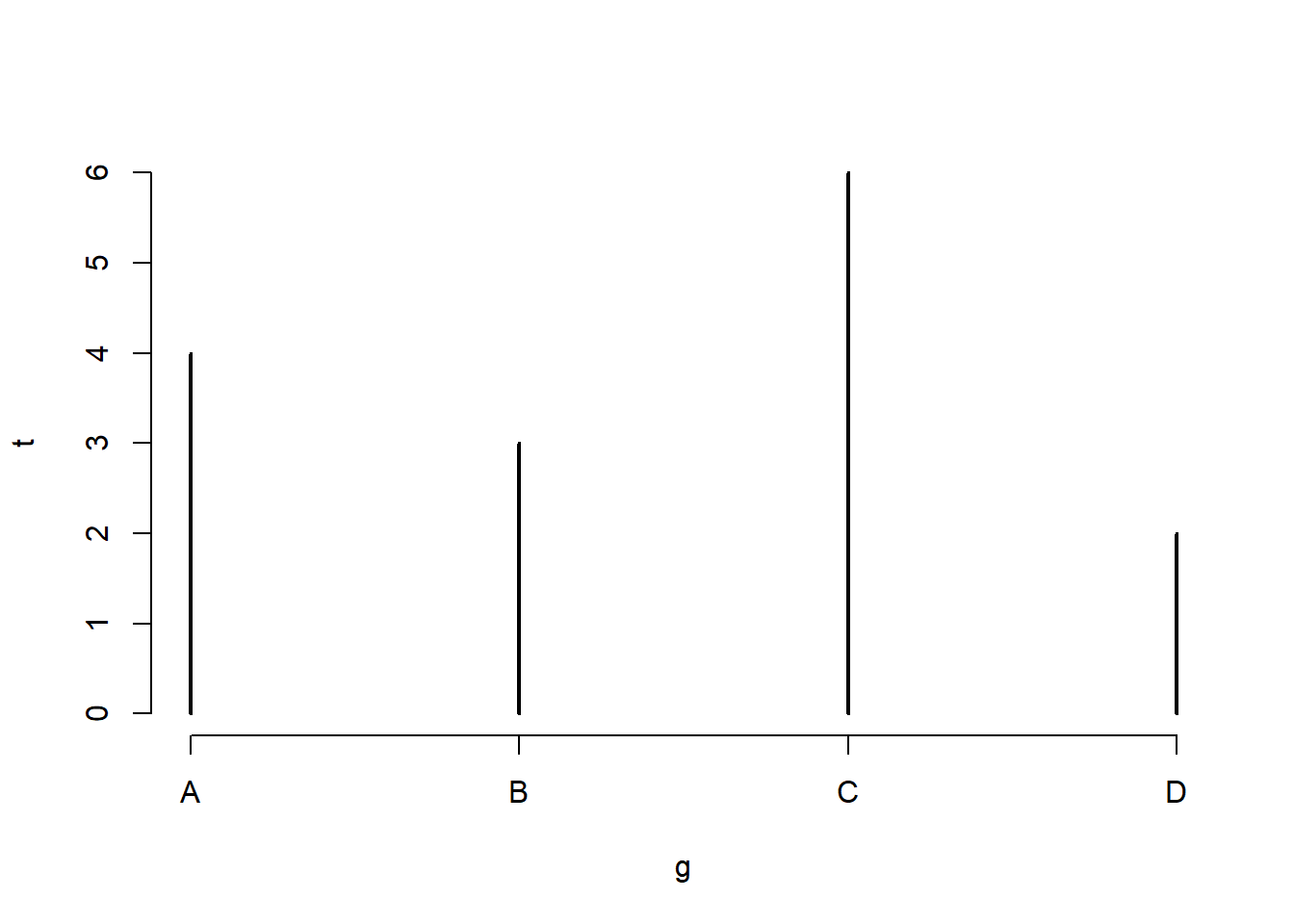
Atkreipkite dėmesį į ašių pavadinimus: abscisė pavadinta pagal vektoriaus vardą, o ordinatė - pagal lentelės objekto vardą.

Stulpelinį, reikšmių dažnių grafiką galima gauti ir greičiau, praleidžiant dažnių lentelės kūrimą. Užtenka raidžių reikšmių vektorių g paversti faktoriumi ir perduoti jį tiesiogiai funkcijai plot().

g <- factor(g)
plot(g)

Jeigu funkcijos plot() parametrui x priskiriamas skaitinis vektorius, o parametrui y – kategorinis (faktorius), tai skirtingoms grupėms priklausančios skaitinio kintamajo reikšmės išdėstomos ant tas grupes atitinkančių horizontalių tiesių.

skaitinis <- c(0.6, 3.4, 6.1, 0.7, 5.2, 1.4, 2.3, 3.4, 2.5, 9.4, 2.7, 4.1, 2.9, 0.1, 7.5)
kategorinis <- c("T", "N", "N", "T", "T", "T", "N", "T", "T", "N", "T", "N", "T", "T", "N")

kategorinis <- factor(kategorinis, levels = c("T", "N"), labels = c("Taip", "Ne"))

plot(skaitinis, kategorinis)

Jeigu parametrui x priskiriamas kategorinis (faktorius) vektorius, o parametrui y – skaitinis, tai iš skirtingoms grupėms priklausančių skaitinio kintamajo reikšmių sudaromos atskiros tų kategorijų boxplot diagramos.

plot(kategorinis, skaitinis)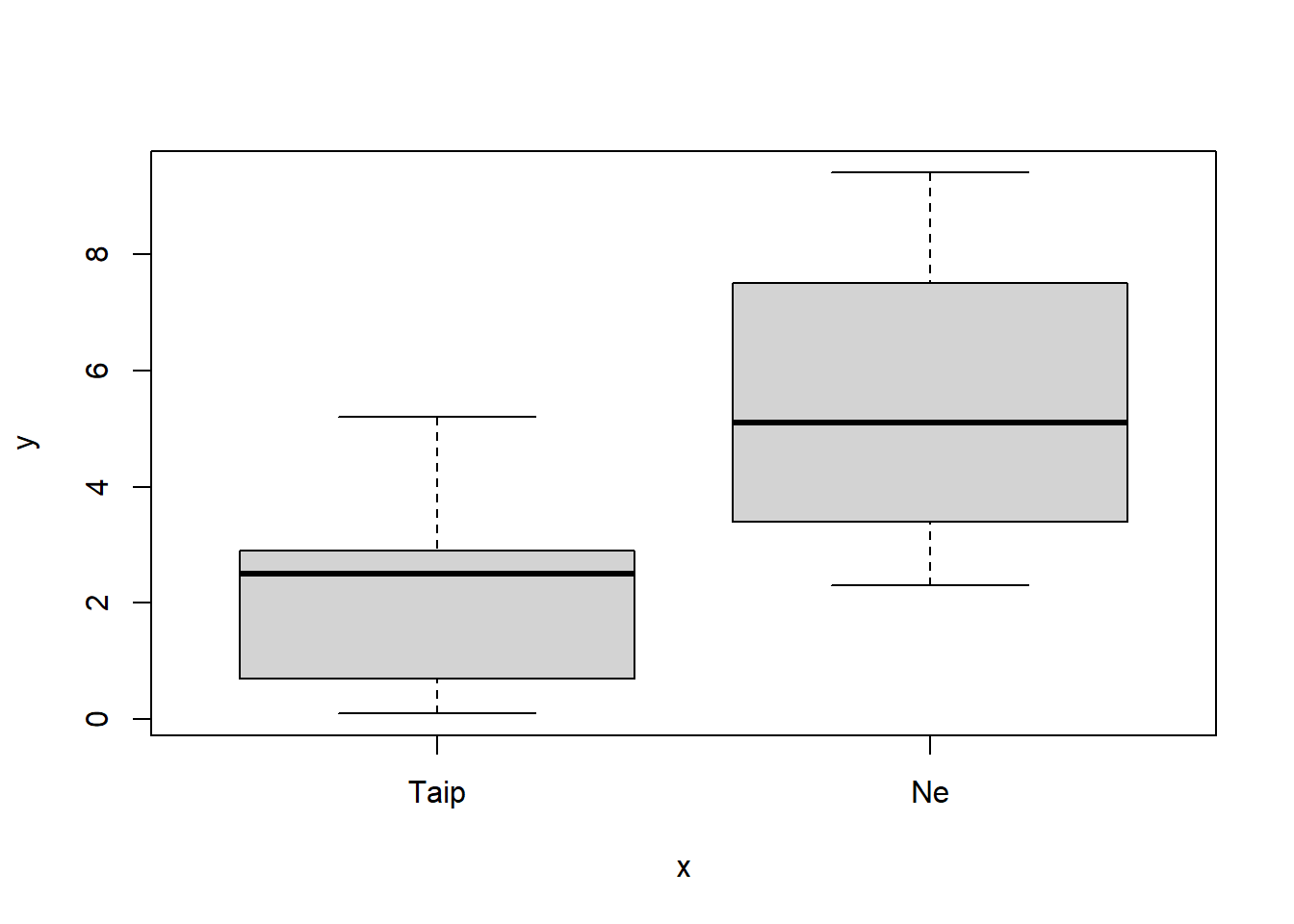

Jei iš karto abiems parametrams x ir y priskiriami kategoriniai kintamieji, nubraižoma speficinė stulpelinė diagrama, kuri vadinama spineplot. Joje ant \(Ox\) ašies išdėstomi skirtingas x kintamąjo kategorijas atitinkantys vienetinio aukščio stulpeliai. Kiekvienas stulpelis padalinamas į tiek dalių, kiek skirtingų y reikšmių yra toje stulpelio grupėje, o dalies dydis proporcingas tų reikšmių dažniui.

prop.table(table(g, kategorinis), margin = 2)
#>    kategorinis
#> g        Taip        Ne
#>   A 0.3333333 0.1666667
#>   B 0.1111111 0.3333333
#>   C 0.4444444 0.3333333
#>   D 0.1111111 0.1666667
plot(kategorinis, g)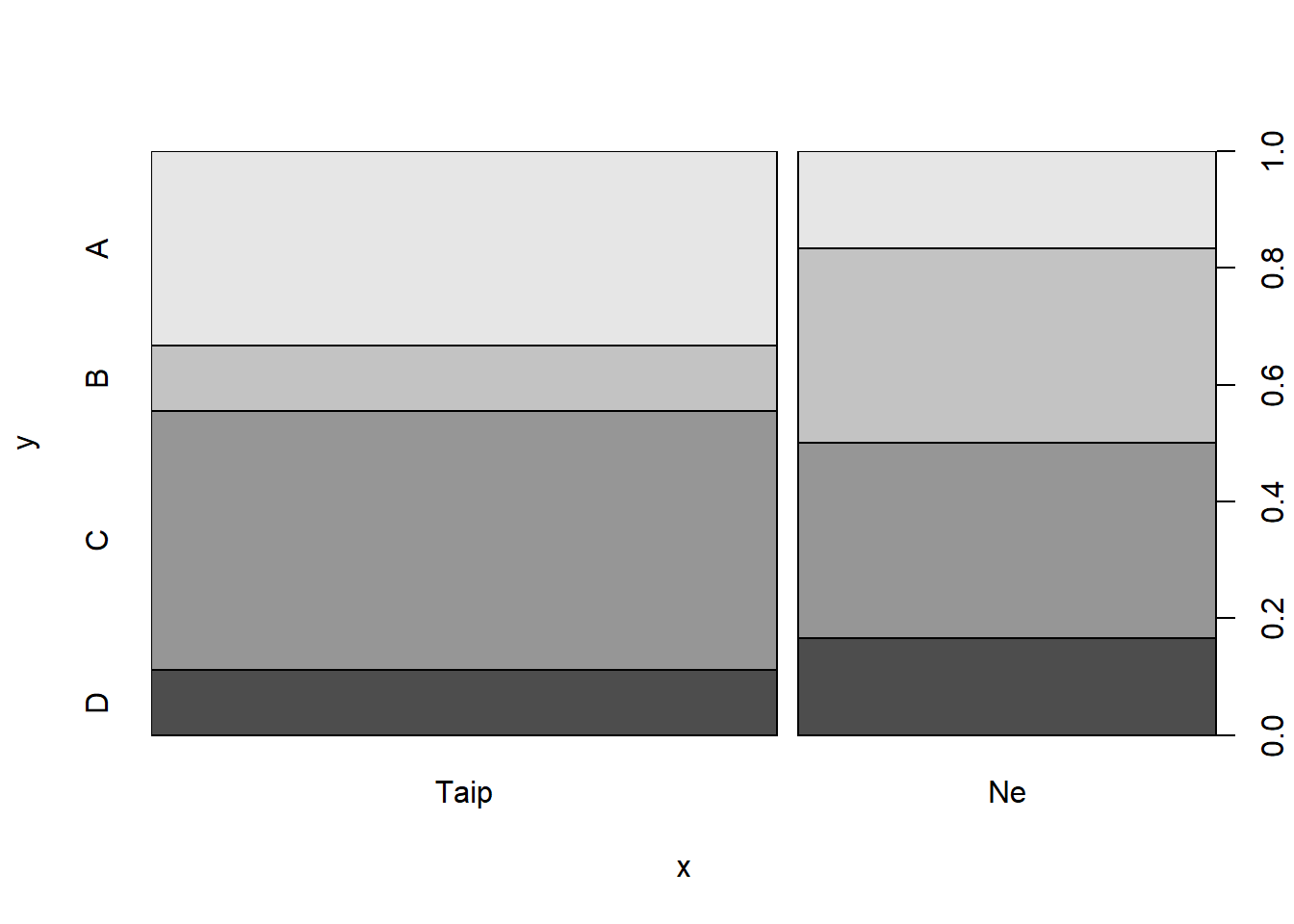

Prieš tai aprašytame skyrelyje formulės metodui galima taikyti ir kategorinius kintamuosius. Tokiu atveju dešinėje modelio pusėje įrašytas kategorinis kintamasis grupuoja kairės pusės kintamojo stebinius. Diagramos pavidalas priklauso nuo to, kokio tipo kintamieji yra vienoje ir kitoje modelio pusėje. Tarkime, kad kintamasis x yra skaitinis, o kintamieji k ir g – kategoriniai (faktoriai). Tokiu atveju galima užrašyti dažniausiai naudojamus modelius:

• ~ k – kategorinio kintamojo k stulpelinė dažnių diagrama,

• x ~ k – skaitinio kintamojo x boxplot diagrama kintamojo k grupėse,

• ~ k + x – skaitinio kintamojo x boxplot diagrama kintamojo k grupėse,

• g ~ k – kategorinio kintamojo g spineplot diagrama grupėse pagal k,

• ~ k + g – kategorinio kintamojo g spineplot diagrama grupėse pagal k.

Nubraižysime skaitinio kintamojo skaitinis boxplot diagramas grupėse suformuotas pagal skirtingas kintamojo kategorinis reikšmes.

plot(skaitinis ~ kategorinis)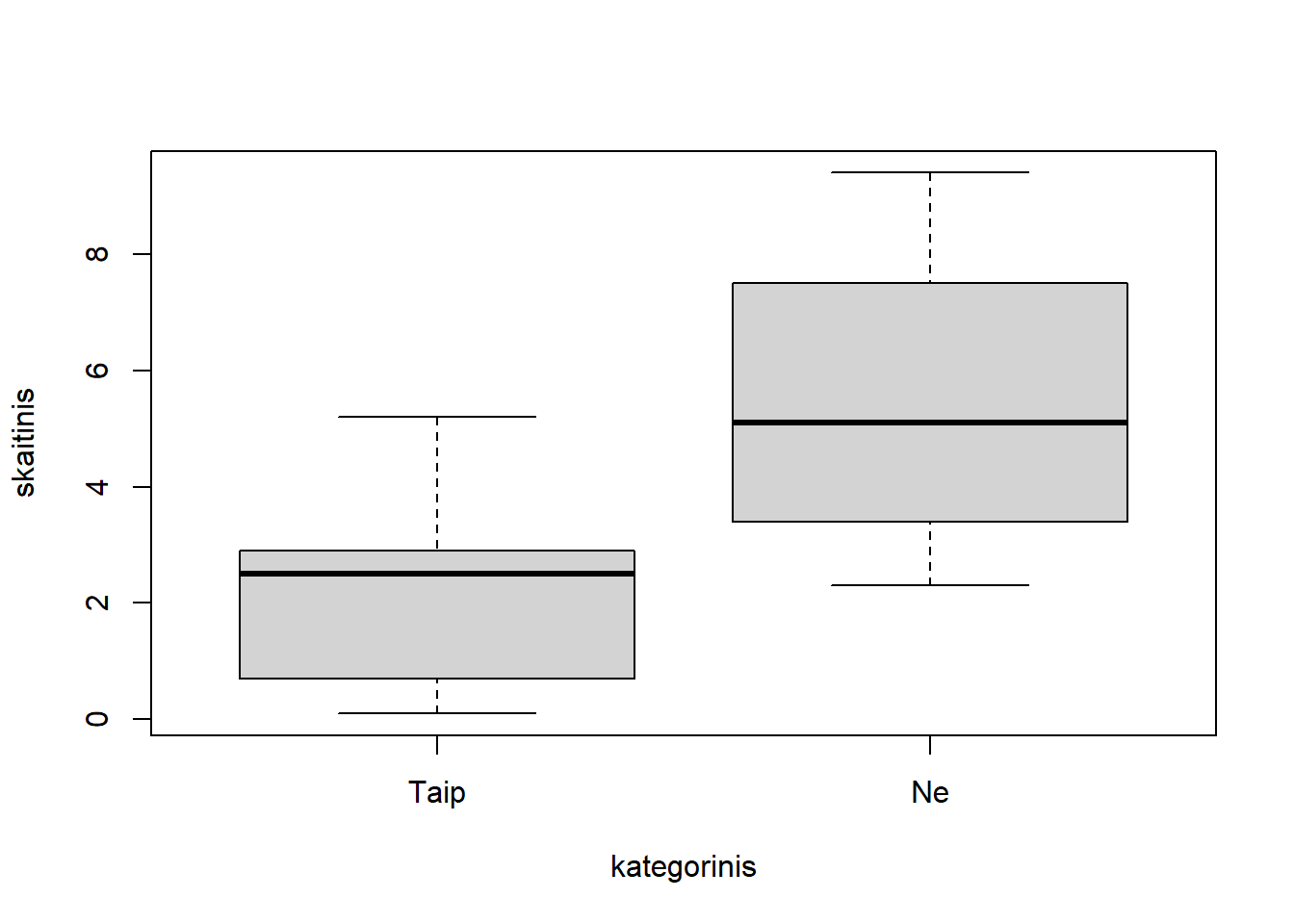

Naudojant modelį, nubraižysime kategorinio kintamojo g dažnių diagramą.

plot( ~ g)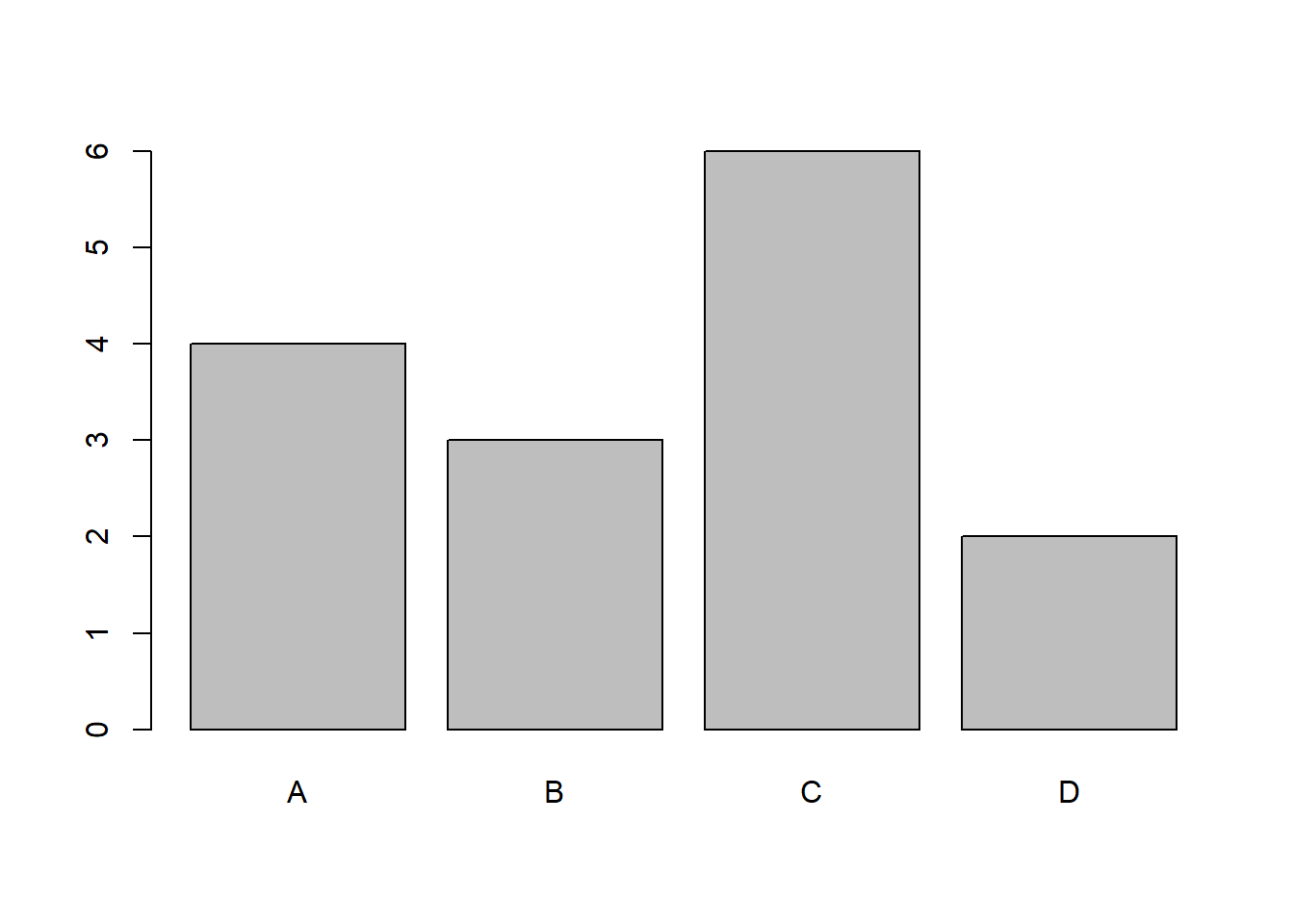

Dviejų kategorinių kintamųjų spineplot diagramą galima nubraižyti užrašant du ekvivalenčius jų priklausomybės modelius. Galima atkreipti dėmesį, kad pirmas kintamasis dešinėje visada yra grupuojantis. Šiuo atveju tai yra kintamasis g.

plot(kategorinis ~ g)

plot(  ~ g + kategorinis)

Užduotis

Sąlyga

1. Sudarykite vektorių iš šios užduoties pirmojo sakinio raidžių (ieškokite funkcijos strsplit()). Visos raidės vektoriuje turi būti arba mažosios, arba didžiosios. Sudarykite raidžių dažnių lentelę, išrikiuokite didėjimo tvarka dažnius ir atvaizduokite lentelę kaip stulpelinę diagramą.

2. Pirmoje užduotyje sudarytą raidžių vektorių paverskite į faktorių. Gaukite tokią pačią raidžių pasikartojimo dažnių stulpelinę diagramą:

1. nenaudojant kategorinio kintamojo sklaidos modelio,

2. naudojant modelį.

3. Naudojant pirmoje užduotyje sudarytą raidžių vektorių, sudarykite papildomą vektorių, kurio elementams priskiriama reikšmė “B”, jei raidė yra balsė, ir reikšmė “P”, jei raidė yra priebalsė. Paverskite šį vektorių į kategorinį kintamąjį. Atvaizduokite balsių ir priebalsių dažnių diagramą ir atsakykite, kokių raidžių yra daugiau?

4. Užrašykite tokį kintamųjų sąryšio modelį, kad pagal jį būtų galima nubrėžti duomenų lentelės iris kintamojo Sepal.Length boxplot diagramas atskirai kiekvienai kategorinio kintamojo Species grupei.