Kodas
plot.new()Bet kokio sudėtingumo grafiko braižymas susideda iš keletos pagrindinių etapų: grafinio įrenginio atidarymo, koordinačių sistemos sudarymo, taškų arba linijų koordinačių skaičiavimo ir jų atidėjimo grafiniame lange. Visus šiuos veiksmus atlieka tokios funkcijos:
plot.new() – sustabdo grafiko braižymą viename lange ir sukuria naują,plot.window() – grafiniame lange sukuria koordinačių sistemą,xy.coords() – apskaičiuoja taškų grafiniame lange koordinates,plot.xy() – grafiniame lange atideda taškus,plot.default() – bazinė aukšto lygio grafinė funkcija.Pagrindinė aukšto lygio grafinė funkcija – plot(), kuri turi keletą metodų. Jos rezultatas priklauso nuo argumento. Jei argumentas yra taškai su koordinatėmis \((x, y)\), tai grafiko braižymas perduodamas funkcijai plot.default(), kuri taškams grafike atidėti naudoja funkciją plot.xy(). šios funkcijos argumentas – sąrašas iš keturių elementų: taškų koordinatės \(x\) ir \(y\) ir koordinačių ašių pavadinimai. Tada taškai atidedami grafiniame lange su nustatyta koordinačių sistema. Tokiu būdu susidaro tam tikra funkcijų seka, kuri atspindi grafiko braižymo etapus (žr. iliustraciją).
Visos aukšto lygio grafinės funkcijos, tokios kaip plot(), curve(), hist() ir kitos, grafiką braižo arba naujame grafiniame lange, arba anksčiau atidarytame lange, kuris prieš tai išvalomas. šiuos veiksmus, prieš grafiko braižymą aukšto lygio grafine f-ja, automatiškai atlieka funkcija plot.new().
Pavyzdžiui, jeigu nėra nei vieno grafinio lango, funkcija plot.new() jį atidaro.
plot.new()Jeigu grafinis langas atidarytas, nepriklausomai nuo to, kas jame pavaizduota, funkcija plot.new() jį išvalo.
Funkcijos plot.new() sukurtame grafiniame lange koordinačių ašių ribos yra nuo 0 iki 1. Tuo nesunku įsitikinti naujame grafiniame lange nubraižius ašis.
Koordinačių sistemos sudarymui naudojama funkcija plot.window().
| Argumentas | Reikšmė |
|---|---|
xlim |
ašies \(Ox\) ribos |
ylim |
ašies \(Oy\) ribos |
asp |
koordinačių santykis \(y/x\) |
Pavyzdžiui, atidarysime naują grafinį langą ir jame nustatysime reikiamas ašių ribas: \(Ox\) intervalas \([10, 20]\) ir \(Oy\) intervalas \([0, 5]\).
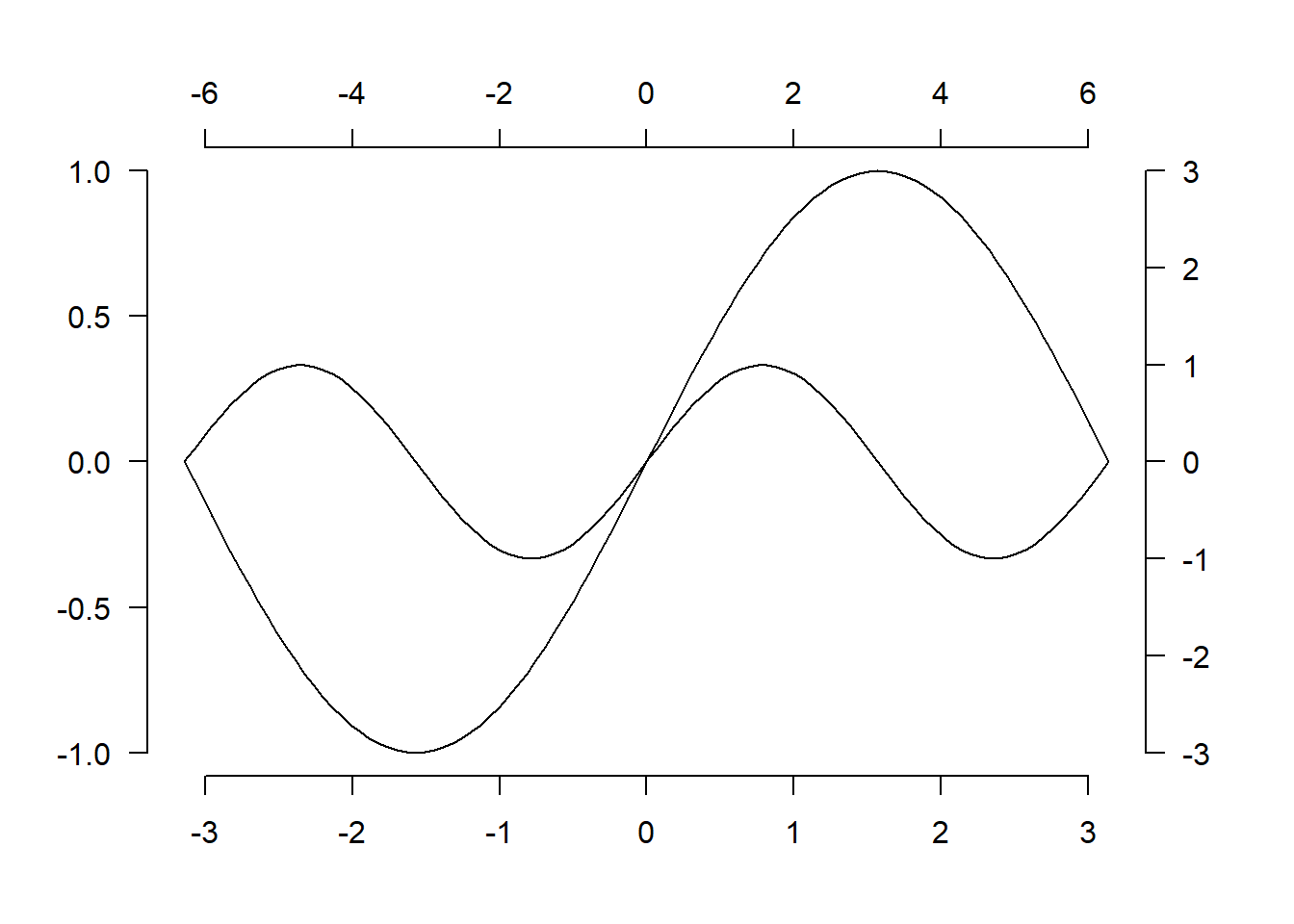
Taip galima pakeisti ir jau nubraižyto grafiko koordinačių sistemą. Pavyzdžiui, nubraižysime funkcijos \(y = \sin x\) grafiką įprastoje koordinačių sistemoje, kur ašies \(Oy\) intervalas \([-1, 1]\). Pakeitus koordinačių sistemą tos pačios funkcijos grafikas atrodo visiškai kitaip.
Funkcija xy.coords() sudaro sąrašą su taškų koordinatėmis \((x, y)\) bei koordinačių ašių pavadinimais: x, y, xlab ir ylab. Šis sąrašas naudojamas taškų atidėjimui grafike, kurį atlieka bazinė taškų ir linijų braižymo funkcija plot.xy(), tačiau prieš tai aptarsime f-jos xy.coords() parametrus.
| Argumentas | Reikšmė |
|---|---|
x |
taškų \(x\) koordinačių vektorius |
y |
taškų \(y\) koordinačių vektorius |
xlab |
\(Ox\) ašies pavadinimas |
ylab |
\(Oy\) ašies pavadinimas |
log |
nurodo, kuri ašis logaritminėje skalėje |
recycle |
nurodo, ar trumpesnį koordinačių vektorių cikliškai pratæsti |
Pavyzdžiui, turėdami taškų koordinačių vektorius, sukursime tų taškų braižymui reikalinga sąrašą su taškų koordinatėmis ir koordinačių ašių pavadinimais.
x <- seq(-pi, pi, length = 100)
y <- sin(x)
xy.coords(x, y, xlab = "x", ylab = "sin(x)")
#> $x
#> [1] -3.14159265 -3.07812614 -3.01465962 -2.95119310 -2.88772658 -2.82426006
#> [7] -2.76079354 -2.69732703 -2.63386051 -2.57039399 -2.50692747 -2.44346095
#> [13] -2.37999443 -2.31652792 -2.25306140 -2.18959488 -2.12612836 -2.06266184
#> [19] -1.99919533 -1.93572881 -1.87226229 -1.80879577 -1.74532925 -1.68186273
#> [25] -1.61839622 -1.55492970 -1.49146318 -1.42799666 -1.36453014 -1.30106362
#> [31] -1.23759711 -1.17413059 -1.11066407 -1.04719755 -0.98373103 -0.92026451
#> [37] -0.85679800 -0.79333148 -0.72986496 -0.66639844 -0.60293192 -0.53946541
#> [43] -0.47599889 -0.41253237 -0.34906585 -0.28559933 -0.22213281 -0.15866630
#> [49] -0.09519978 -0.03173326 0.03173326 0.09519978 0.15866630 0.22213281
#> [55] 0.28559933 0.34906585 0.41253237 0.47599889 0.53946541 0.60293192
#> [61] 0.66639844 0.72986496 0.79333148 0.85679800 0.92026451 0.98373103
#> [67] 1.04719755 1.11066407 1.17413059 1.23759711 1.30106362 1.36453014
#> [73] 1.42799666 1.49146318 1.55492970 1.61839622 1.68186273 1.74532925
#> [79] 1.80879577 1.87226229 1.93572881 1.99919533 2.06266184 2.12612836
#> [85] 2.18959488 2.25306140 2.31652792 2.37999443 2.44346095 2.50692747
#> [91] 2.57039399 2.63386051 2.69732703 2.76079354 2.82426006 2.88772658
#> [97] 2.95119310 3.01465962 3.07812614 3.14159265
#>
#> $y
#> [1] -1.224606e-16 -6.342392e-02 -1.265925e-01 -1.892512e-01 -2.511480e-01
#> [6] -3.120334e-01 -3.716625e-01 -4.297949e-01 -4.861967e-01 -5.406408e-01
#> [11] -5.929079e-01 -6.427876e-01 -6.900790e-01 -7.345917e-01 -7.761465e-01
#> [16] -8.145760e-01 -8.497254e-01 -8.814534e-01 -9.096320e-01 -9.341479e-01
#> [21] -9.549022e-01 -9.718116e-01 -9.848078e-01 -9.938385e-01 -9.988673e-01
#> [26] -9.998741e-01 -9.968548e-01 -9.898214e-01 -9.788024e-01 -9.638422e-01
#> [31] -9.450008e-01 -9.223543e-01 -8.959938e-01 -8.660254e-01 -8.325699e-01
#> [36] -7.957618e-01 -7.557496e-01 -7.126942e-01 -6.667690e-01 -6.181590e-01
#> [41] -5.670599e-01 -5.136774e-01 -4.582265e-01 -4.009305e-01 -3.420201e-01
#> [46] -2.817326e-01 -2.203105e-01 -1.580014e-01 -9.505604e-02 -3.172793e-02
#> [51] 3.172793e-02 9.505604e-02 1.580014e-01 2.203105e-01 2.817326e-01
#> [56] 3.420201e-01 4.009305e-01 4.582265e-01 5.136774e-01 5.670599e-01
#> [61] 6.181590e-01 6.667690e-01 7.126942e-01 7.557496e-01 7.957618e-01
#> [66] 8.325699e-01 8.660254e-01 8.959938e-01 9.223543e-01 9.450008e-01
#> [71] 9.638422e-01 9.788024e-01 9.898214e-01 9.968548e-01 9.998741e-01
#> [76] 9.988673e-01 9.938385e-01 9.848078e-01 9.718116e-01 9.549022e-01
#> [81] 9.341479e-01 9.096320e-01 8.814534e-01 8.497254e-01 8.145760e-01
#> [86] 7.761465e-01 7.345917e-01 6.900790e-01 6.427876e-01 5.929079e-01
#> [91] 5.406408e-01 4.861967e-01 4.297949e-01 3.716625e-01 3.120334e-01
#> [96] 2.511480e-01 1.892512e-01 1.265925e-01 6.342392e-02 1.224606e-16
#>
#> $xlab
#> [1] "x"
#>
#> $ylab
#> [1] "sin(x)"Koordinačių vektorius galima susieti per formulę y ~ x.
xy.coords(y ~ x, xlab = "x", ylab = "sin(x)")
#> $x
#> [1] -3.14159265 -3.07812614 -3.01465962 -2.95119310 -2.88772658 -2.82426006
#> [7] -2.76079354 -2.69732703 -2.63386051 -2.57039399 -2.50692747 -2.44346095
#> [13] -2.37999443 -2.31652792 -2.25306140 -2.18959488 -2.12612836 -2.06266184
#> [19] -1.99919533 -1.93572881 -1.87226229 -1.80879577 -1.74532925 -1.68186273
#> [25] -1.61839622 -1.55492970 -1.49146318 -1.42799666 -1.36453014 -1.30106362
#> [31] -1.23759711 -1.17413059 -1.11066407 -1.04719755 -0.98373103 -0.92026451
#> [37] -0.85679800 -0.79333148 -0.72986496 -0.66639844 -0.60293192 -0.53946541
#> [43] -0.47599889 -0.41253237 -0.34906585 -0.28559933 -0.22213281 -0.15866630
#> [49] -0.09519978 -0.03173326 0.03173326 0.09519978 0.15866630 0.22213281
#> [55] 0.28559933 0.34906585 0.41253237 0.47599889 0.53946541 0.60293192
#> [61] 0.66639844 0.72986496 0.79333148 0.85679800 0.92026451 0.98373103
#> [67] 1.04719755 1.11066407 1.17413059 1.23759711 1.30106362 1.36453014
#> [73] 1.42799666 1.49146318 1.55492970 1.61839622 1.68186273 1.74532925
#> [79] 1.80879577 1.87226229 1.93572881 1.99919533 2.06266184 2.12612836
#> [85] 2.18959488 2.25306140 2.31652792 2.37999443 2.44346095 2.50692747
#> [91] 2.57039399 2.63386051 2.69732703 2.76079354 2.82426006 2.88772658
#> [97] 2.95119310 3.01465962 3.07812614 3.14159265
#>
#> $y
#> [1] -1.224606e-16 -6.342392e-02 -1.265925e-01 -1.892512e-01 -2.511480e-01
#> [6] -3.120334e-01 -3.716625e-01 -4.297949e-01 -4.861967e-01 -5.406408e-01
#> [11] -5.929079e-01 -6.427876e-01 -6.900790e-01 -7.345917e-01 -7.761465e-01
#> [16] -8.145760e-01 -8.497254e-01 -8.814534e-01 -9.096320e-01 -9.341479e-01
#> [21] -9.549022e-01 -9.718116e-01 -9.848078e-01 -9.938385e-01 -9.988673e-01
#> [26] -9.998741e-01 -9.968548e-01 -9.898214e-01 -9.788024e-01 -9.638422e-01
#> [31] -9.450008e-01 -9.223543e-01 -8.959938e-01 -8.660254e-01 -8.325699e-01
#> [36] -7.957618e-01 -7.557496e-01 -7.126942e-01 -6.667690e-01 -6.181590e-01
#> [41] -5.670599e-01 -5.136774e-01 -4.582265e-01 -4.009305e-01 -3.420201e-01
#> [46] -2.817326e-01 -2.203105e-01 -1.580014e-01 -9.505604e-02 -3.172793e-02
#> [51] 3.172793e-02 9.505604e-02 1.580014e-01 2.203105e-01 2.817326e-01
#> [56] 3.420201e-01 4.009305e-01 4.582265e-01 5.136774e-01 5.670599e-01
#> [61] 6.181590e-01 6.667690e-01 7.126942e-01 7.557496e-01 7.957618e-01
#> [66] 8.325699e-01 8.660254e-01 8.959938e-01 9.223543e-01 9.450008e-01
#> [71] 9.638422e-01 9.788024e-01 9.898214e-01 9.968548e-01 9.998741e-01
#> [76] 9.988673e-01 9.938385e-01 9.848078e-01 9.718116e-01 9.549022e-01
#> [81] 9.341479e-01 9.096320e-01 8.814534e-01 8.497254e-01 8.145760e-01
#> [86] 7.761465e-01 7.345917e-01 6.900790e-01 6.427876e-01 5.929079e-01
#> [91] 5.406408e-01 4.861967e-01 4.297949e-01 3.716625e-01 3.120334e-01
#> [96] 2.511480e-01 1.892512e-01 1.265925e-01 6.342392e-02 1.224606e-16
#>
#> $xlab
#> [1] "x"
#>
#> $ylab
#> [1] "y"Loginiam parametrui recycle priskiriant reikšmę TRUE, nustatome, kad trumpesnį koordinačių vektorių galima cikliškai pratęsti ir tokiu būdu juos suvienodinti.
xy.coords(1:10, 1:2, xlab = "x", ylab = "y", recycle = TRUE)
#> $x
#> [1] 1 2 3 4 5 6 7 8 9 10
#>
#> $y
#> [1] 1 2 1 2 1 2 1 2 1 2
#>
#> $xlab
#> [1] "x"
#>
#> $ylab
#> [1] "y"Naudojant funkcijos xy.coords() sudarytą sąrašą, funkcija plot.xy() atideda taškus grafiniame lange su nustatyta koordinačių sistema. Pagrindiniai jos parametrai išvardyti žemiau.
| Argumentas | Reikšmė |
|---|---|
xy |
sąrašas su taškų koordinatėmis ir ašių pavadinimais |
type |
diagramos tipas |
pch |
taško simbolis arba jo numeris |
lty |
linijos tipas |
lwd |
linijos storis |
col |
linijos arba taško spalva |
cex |
taško mastelio koeficientas |
Pavyzdžiui, sudarysime taškų koordinačių sąrašą ir, naudojant funkciją plot.xy() nubraižysime taškų sklaidos diagramą iš anksto atidarytame grafiniame lange su nustatyta koordinačių sistema.
x <- c(2.0, 1.6, 1.2, 0.9, 1.0, 1.3, 1.6, 2.0, 2.3, 2.8, 2.9, 3.0, 2.8, 2.4, 2.1)
y <- c(0.8, 1.1, 1.3, 1.6, 2.2, 2.5, 2.9, 3.1, 3.0, 2.8, 2.4, 1.8, 1.4, 1.0, 0.9)
xy <- xy.coords(x, y, xlab = "x", ylab = "y")
xy
#> $x
#> [1] 2.0 1.6 1.2 0.9 1.0 1.3 1.6 2.0 2.3 2.8 2.9 3.0 2.8 2.4 2.1
#>
#> $y
#> [1] 0.8 1.1 1.3 1.6 2.2 2.5 2.9 3.1 3.0 2.8 2.4 1.8 1.4 1.0 0.9
#>
#> $xlab
#> [1] "x"
#>
#> $ylab
#> [1] "y"
plot.new()
plot.window(xlim = c(0.8, 3.2), ylim = c(0.8, 3.2))
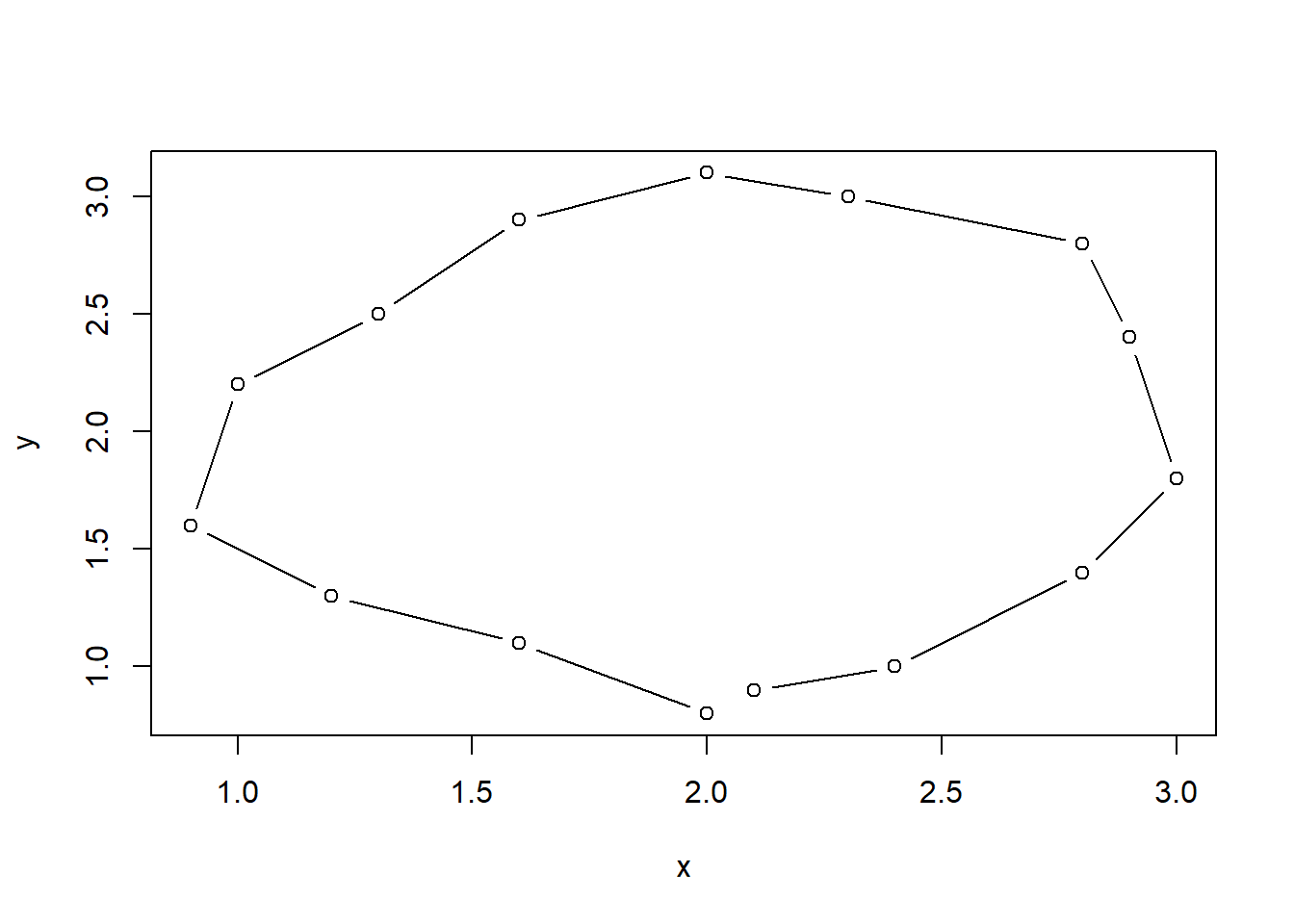
plot.xy(xy, type = "p")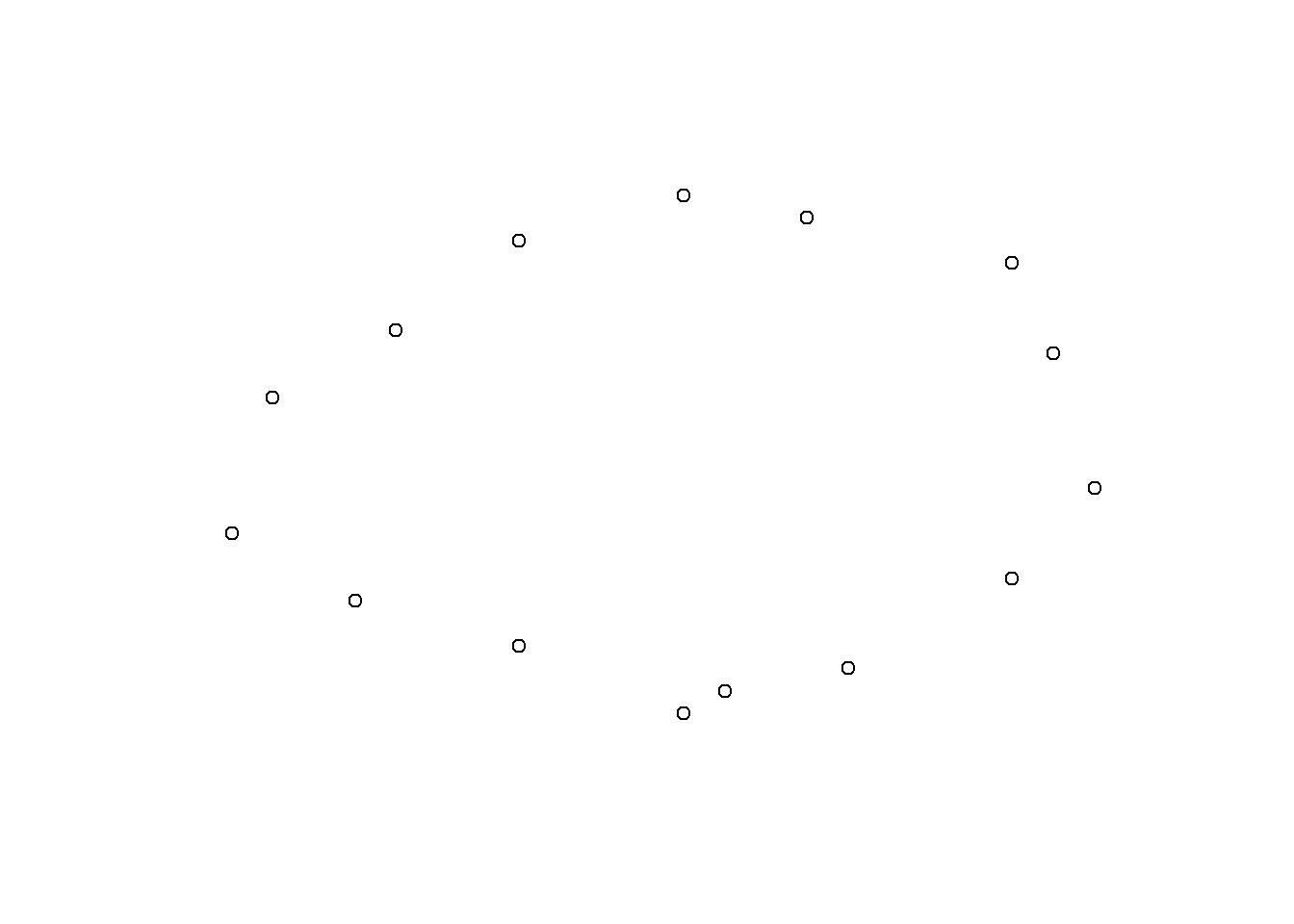
Funkcija plot.xy() nėra aukšto lygio grafinė funkcija, todėl taškus ant anksčiau nubraižyto grafiko atideda jo neištrynusi. Pvz., tuos pačius taškus sujungsime tiesės atkarpomis, tam užtenka pakeisti parametro type reikšmę.
Visą tokiam grafikui nubraižyti reikalingą funkcijų seką pakeičia viena aukšto lygio grafinė funkcija. šiuo atveju tai funkcija plot(). Ji turi metodą sklaidos diagramoms braižyti ir tam naudoja funkciją plot.default(). Pavyzdžiui, tą pačią taškų \((x, y)\) sklaidos diagramą gausime naudojant tam skirtą f-ją plot.default().
plot.default(x, y, type = "b")
Žinoma, toks pat rezultatas gaunamas diagramą braižant su aukšto lygio grafine funkcija plot(), kuri taškų atvaizdavimui ir naudoja f-ją plot.default().
plot(x, y, type = "b")