17  Atsitiktiniai dydžiai ir tikimybiniai skirstiniai

Šiame skyriuje apžvelgiamos kai kurios pagrindinės tikimybių teorijos sąvokos ir paaiškinama, kaip jas galima taikyti su R. Dauguma bazinių statistinių funkcijų yra pakete stats. Tos funkcijos apskaičiuoja aprašomuosius matus ir palengvina skaičiavimus su įvairiais tikimybiniais pasiskirstymais. Jame taip pat yra sudėtingesnių procedūrų, kurios leidžia vartotojui įvertinti daugybę modelių, pagrįstų tais pačiais duomenimis, arba padeda atlikti išsamius simuliacinius tyrimus.

Paketas stats yra bazinio R dalis, o tai reiškia, kad jis yra įdiegtas pagal numatytuosius nustatymus, todėl nereikia vykdyti komandos install.packages(„stats“) arba library(„stats“). Tiesiog vykdykite library(help = „stats“) konsolėje, kad peržiūrėtumėte dokumentaciją ir visą stats funkcijų sąrašą.

Toliau skirsime dėmesio kai kuriems R egzistuojantiems tikimybiniams skirstiniams ir atitinkamų funkcijų naudojimui paprastiems uždaviniams spręsti. Po to apžvelgsime kai kurias pagrindines tikimybių teorijos sąvokas. Be kita ko, išmoksite, kaip generuoti atsitiktinius skaičius, kaip įvertinti tankius, tikimybes, kvantilius ir pan. Kaip pamatysite, šiuos skaičiavimus labai patogu atlikti su R.

17.1 Pagrindinės sąvokos ir apibrėžimai

Šioje konspekto dalyje naudosime keletą tikimybių teorijos sąvokų.

Atsitiktinis dydis (random variable) – tai funkcija, kuri kiekvienam atsitiktinio bandymo baigčiai priskiria realųjį skaičių.
Formaliai, jei \(\Omega\) yra atsitiktinio bandymo baigčių aibė, tai atsitiktinis dydis yra funkcija

\[ X : \Omega \to \mathbb{R}. \]

Atsitiktiniai dydžiai gali būti:

  • diskretūs, kai gali įgyti tik skaitomai daug reikšmių;

  • tolydūs, kai gali įgyti bet kokią reikšmę tam tikrame intervale.

Pasiskirstymo funkcija (cumulative distribution function, CDF) apibrėžiama tiek diskrečiam, tiek tolydžiam atsitiktiniam dydžiui:

\[ F(x) = P(X \le x). \]

Ji parodo tikimybę, kad atsitiktinis dydis \(X\) bus mažesnis arba lygus tam tikrai reikšmei \(x\).

Pasiskirstymo funkcijos savybės:

  • \(F(x)\) yra didėjanti funkcija;

  • \(\displaystyle\lim_{x \to -\infty} F(x) = 0\);

  • \(\displaystyle\lim_{x \to +\infty} F(x) = 1\).

Diskrečiojo a.d. \(X\) pasiskirstymo funkcija apibrėžiama taip: \[ \sum_{x} p(x) = \sum_{x} P(X = x) = 1, \quad p(x) \ge 0. \]

Tolydžiojo a.d. \(X\) atveju pasiskirstymo funkcija:

\[ F(x) = \int_{-\infty}^{x} f(t)\, \mathrm{d}t, \]

kur \(f(x)\) – atitinkama tankio funkcija.

Tolydžiojo atsitiktinio dydžio \(X\) tikimybinio tankio funkcija (probability density function) yra tokia funkcija \(f(x)\), kad:

\[ P(a \le X \le b) = \int_{a}^{b} f(x)\,dx, \] kur \[ f(x) \ge 0, \quad \int_{-\infty}^{\infty} f(x)\,dx = 1. \]

Kvantilis (quantile) – tai reikšmė \(q_p\), tenkinanti sąlygą:

\[ P(X \le q_p) = p, \] kur \(p \in (0,1)\).

Pavyzdžiui, \(p = 0.5\) atitinka medianą.

Tikėtinoji reikšmė arba vidurkis (expectation, mean) – tai atsitiktinio dydžio vidutinė reikšmė, nusakanti jo pasiskirstymo centrinę padėtį.

Diskrečiojo a.d. atveju: \[ E[X] = \sum_{x} x\,p(x). \]

Tolydžiojo a.d. atveju: \[ E[X] = \int_{-\infty}^{\infty} x\,f(x)\,dx. \]

Dispersija (variance) parodo, atsitiktinio dydžio reikšmių sklaidą nuo vidurkio:

\[ Var(X) = E\left[ (X - E[X])^2 \right]. \]

Diskrečiojo a.d. atveju: \[ Var(X) = \sum_{x} (x - E[X])^2 \, p(x), \] tolydžiojo a.d. atveju: \[ Var(X) = \int_{-\infty}^{\infty} (x - E[X])^2 \,f(x)\, \mathrm{d}x. \]

Standartinis nuokrypis (standard deviation) – tai dispersijos kvadratinė šaknis:

\[ \sigma_X = \sqrt{Var(X)}. \]

Jis parodo, kokiu vidutiniu atstumu reikšmės nukrypsta nuo vidurkio.

Koreliacija (correlation) – tai dviejų atsitiktinių dydžių \(X\) ir \(Y\) tiesinio ryšio stiprumo matas.

Pirmiausia apibrėžiama kovariacija: \[ Cov(X, Y) = E[(X - E[X])(Y - E[Y])]. \]

Tada koreliacijos koeficientas: \[ \rho_{XY} = \frac{Cov(X, Y)}{\sigma_X \sigma_Y}, \] kur \(-1 \le \rho_{XY} \le 1\).

Kai \(\rho_{XY} = 1\) – tobulas teigiamas ryšys,
kai \(\rho_{XY} = -1\) – tobulas neigiamas ryšys,
kai \(\rho_{XY} = 0\) – tiesinis ryšys neegzistuoja.

17.2 Tikimybiniai skirstiniai

Kiekvienas bazinio R tikimybinis skirstinys turi keturias funkcijas. Pavyzdžiui, binominis skirstinys turi funkcijas pbinom, dbinom, qbinom ir rbinom. Šių funkcijų pavadinimai sudaromi pagal skirstinio šaknį (pvz. binom) ir priešdėlius:

  • p - atitinka žodį probability, pasiskirstymo funkcija,

  • d - atitinka žodį density, tikimybinės masės (diskrečių a.d.) arba tankio funkcija (tolydžių a.d.),

  • q - atitinka žodį quantile, kvantilių funkcija,

  • r - atitinka žodį random, atitinkamo pasiskirstymo dėsnio atsitiktinių dydžių generavimo funkcija.

Su normaliuoju skirstiniu susijusios funkcijos būtų pnorm, dnorm, qnorm ir rnorm. Bazinis R turi funkcijas, skirtas daugeliui tikimybių skirstinių valdyti. Žemiau lentelėje pateikti įvairūs tikimybiniai skirstinai su atitinkamomis R funkcijomis.

Skirstinys Pasiskirstymo funkcija p* Kvantilio funkcija q* Tankio funkcija d* Atsitiktinių dydžių generavimas r*
Beta skirstinys pbeta qbeta dbeta rbeta
Binominis (įskaitant Bernulio) pbinom qbinom dbinom rbinom
Gimtadienio (Birthday) skirstinys pbirthday qbirthday
Koši (Cauchy) skirstinys pcauchy qcauchy dcauchy rcauchy
Chi-kvadrato (Chi-Square) skirstinys pchisq qchisq dchisq rchisq
Diskretus tolygusis skirstinys sample
Eksponentinis skirstinys pexp qexp dexp rexp
Fišerio (F) skirstinys pf qf df rf
Gamma skirstinys pgamma qgamma dgamma rgamma
Geometrinis skirstinys pgeom qgeom dgeom rgeom
Hipergeometrinis skirstinys phyper qhyper dhyper rhyper
Logistinis skirstinys plogis qlogis dlogis rlogis
Log-normalus skirstinys plnorm qlnorm dlnorm rlnorm
Multinominis (multinomial) skirstinys dmultinom rmultinom
Neigiamas binominis skirstinys pnbinom qnbinom dnbinom rnbinom
Normalusis skirstinys pnorm qnorm dnorm rnorm
Puasono (Poisson) skirstinys ppois qpois dpois rpois
Kolmogorovo–Smirnovo statistika psmirnov qsmirnov rsmirnov
Stjudento t skirstinys pt qt dt rt
Stjudentizuoto rėžio (Tukey) skirstinys ptukey qtukey dtukey rtukey
Tolygusis skirstinys punif qunif dunif runif
Weibullo skirstinys pweibull qweibull dweibull rweibull
Vilkoksono rangų sumos statistika pwilcox qwilcox dwilcox rwilcox
Vilkoksono ženklų rangų statistika psignrank qsignrank dsignrank rsignrank
Višarto (Wishart) skirstinys rWishart

Pasiskirstymo funkcija

Tarkime, atsitiktinis dydis \(X \sim Bin(n = 10,\, p = 0.3)\), t. y. atliekame 10 nepriklausomų Bernulio bandymų, kuriuose sėkmės tikimybė yra 0.3.
Pasiskirstymo funkciją galima apskaičiuoti su pbinom(). Funkcijos argumentai atitinka įprastus pasiskirstymo funkcijos parametrus: reikšmių vektorių, bandymų skaičių ir sėkmės tikimybę.

Kodas
x <- 0:10
F_binom <- pbinom(x, size = 10, prob = 0.3)
F_binom
#>  [1] 0.02824752 0.14930835 0.38278279 0.64961072 0.84973167 0.95265101
#>  [7] 0.98940792 0.99840961 0.99985631 0.99999410 1.00000000

Daugelis realizuotų pasiskirstymų funkcijų R turi loginį parametrą lower.tail = TRUE, kuris pagal nutylėjimą tokias tikimybes \(P (X \leq x)\). Jeigu parametras lower.tail = FALSE, tai vertinamos tokios tikimybės \(P (X > x)\).

Kodas
F_binom_upper <- pbinom(x, size = 10, prob = 0.3, lower.tail = F)
F_binom_upper
#>  [1] 0.9717524751 0.8506916541 0.6172172136 0.3503892816 0.1502683326
#>  [6] 0.0473489874 0.0105920784 0.0015903864 0.0001436859 0.0000059049
#> [11] 0.0000000000

Galima nubrėžti a.d. pasiskirsčiusio pagal Binominį dėsnį pasiskirstymo funkcijos grafiką.

Kodas
plot(x, F_binom, type = "s", main = "Binominio skirstinio pasiskirstymo funkcija",
     xlab = "x", ylab = "F(x)", col = "steelblue", lwd = 2)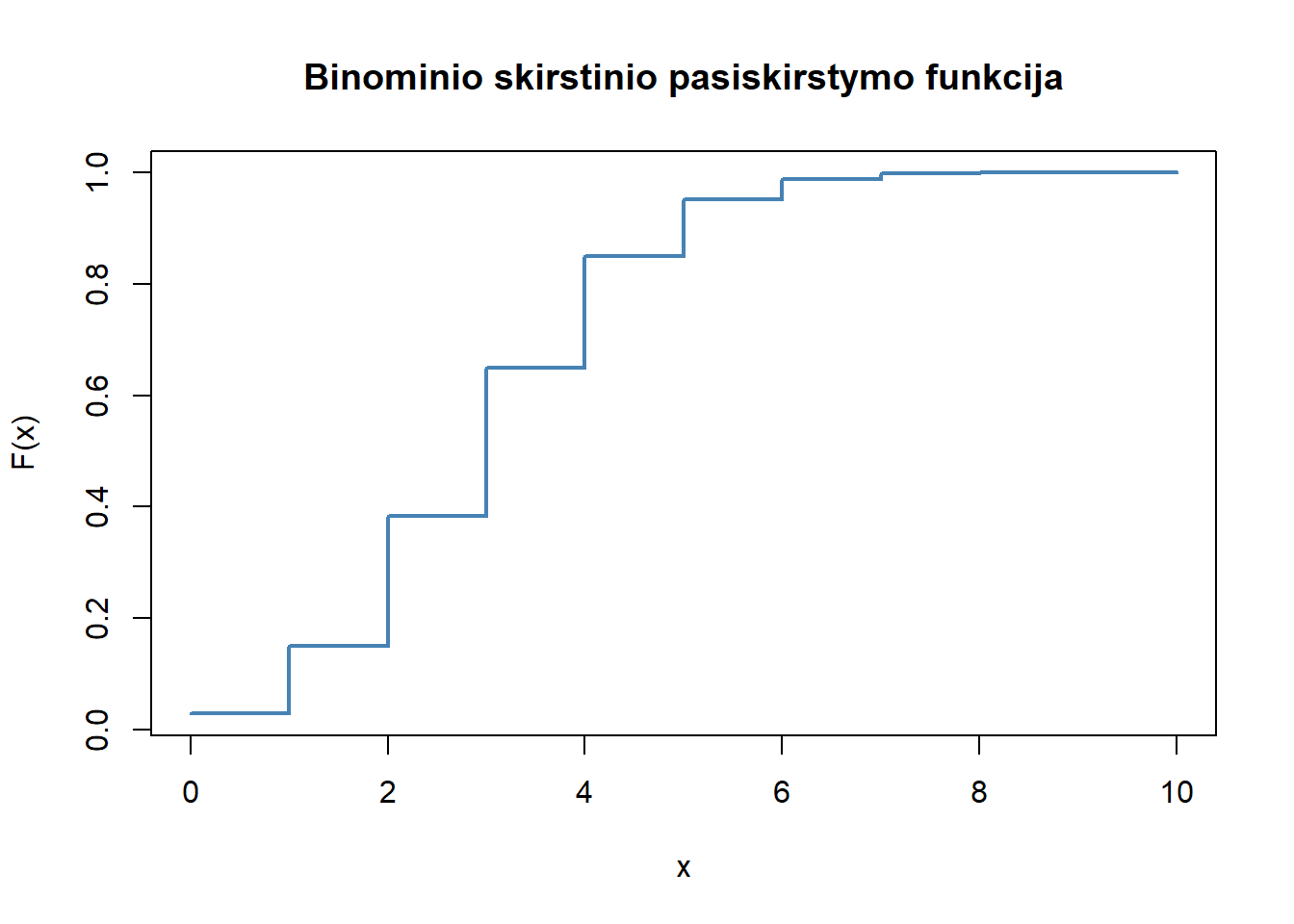

Gauname laiptuotą kreivę, kuri šokteli ties kiekviena galima reikšme \(x\). Kiekvienas šuolis atitinka tikimybę \(P(X=x)\).

Normaliojo atsitiktinio dydžio \(X \sim \mathcal{N}(\mu, \sigma^2)\) pasiskirstymo funkcija yra lygi:

\[ F(x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi\sigma^2}} e^{-(t-\mu)^2 / 2\sigma^2} \,\,\mathrm{d}t \]

R kalboje tokio a.d. pasiskirstymo funkcijos reikšmėms gauti naudojama funkcija pnorm(), kurios parametrai yra \(x\) reikšmių vektorius, vidurkis \(\mu\) ir standartinis nuokrypis \(\sqrt{\sigma^2}\).

Kodas
x <- seq(-4, 4, by = 0.1)
F_norm <- pnorm(x, mean = 0, sd = 1)

Nubraižome pasiskirstymo funkciją. Rezultatas - tolydi kreivė, didėjanti nuo 0 iki 1.

Kodas
plot(x, F_norm, type = "l", main = "Normaliojo skirstinio pasiskirstymo funkcija",
     xlab = "x", ylab = "F(x)", col = "darkgreen", lwd = 2)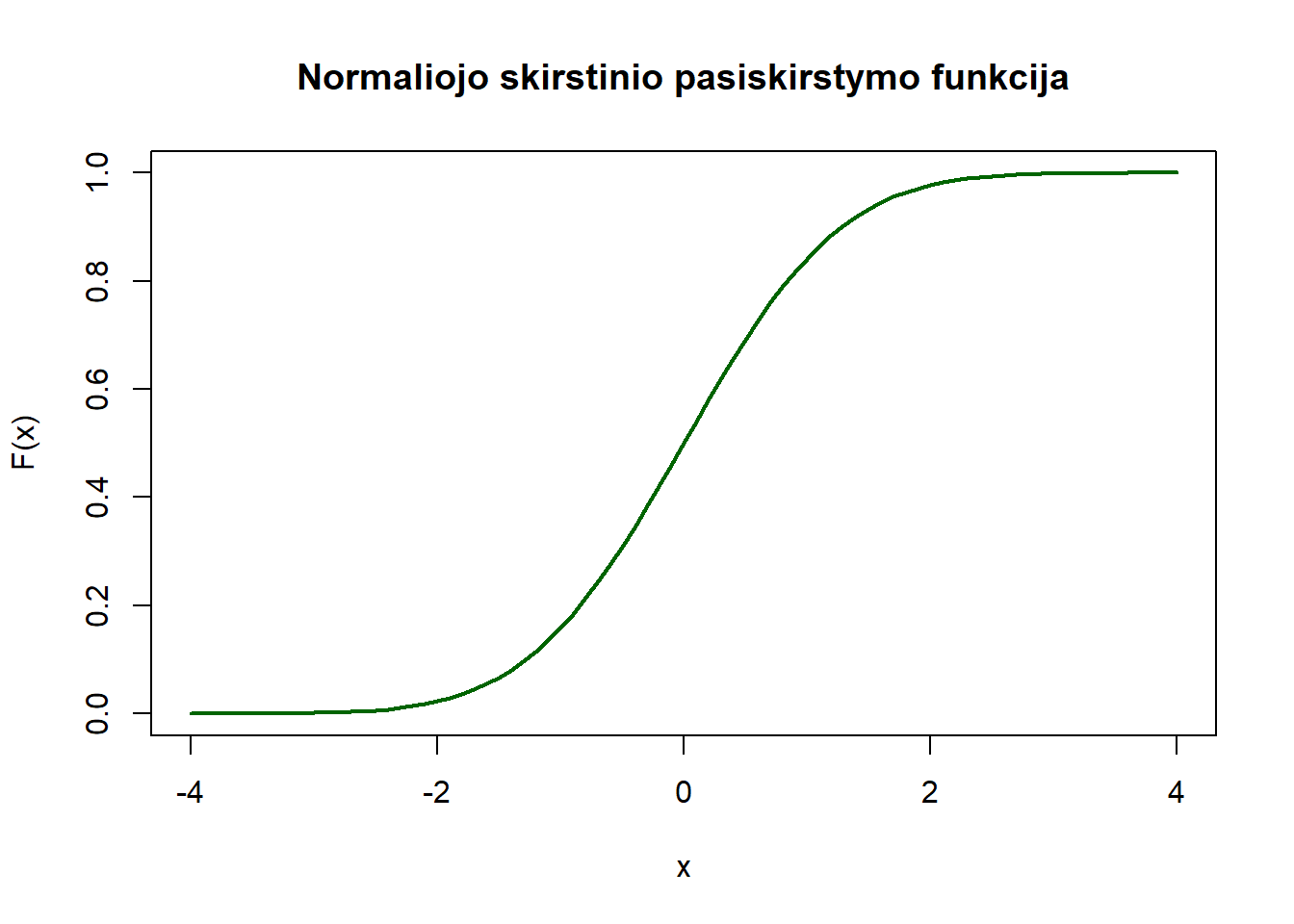

Kadangi pasiskirstymo funkcijos paprasčiausiai yra ne kas kita kaip matematinės funkcijos, tai f-jų grafikus galima gauti naudojant curve().

Kodas
curve(pnorm, 
      from = -4, to = 4, ylab = "F(x)", col = "darkgreen", lwd = 2,
      main = "X ~ N(0, 1) pasiskirstymo funkcija F(x)")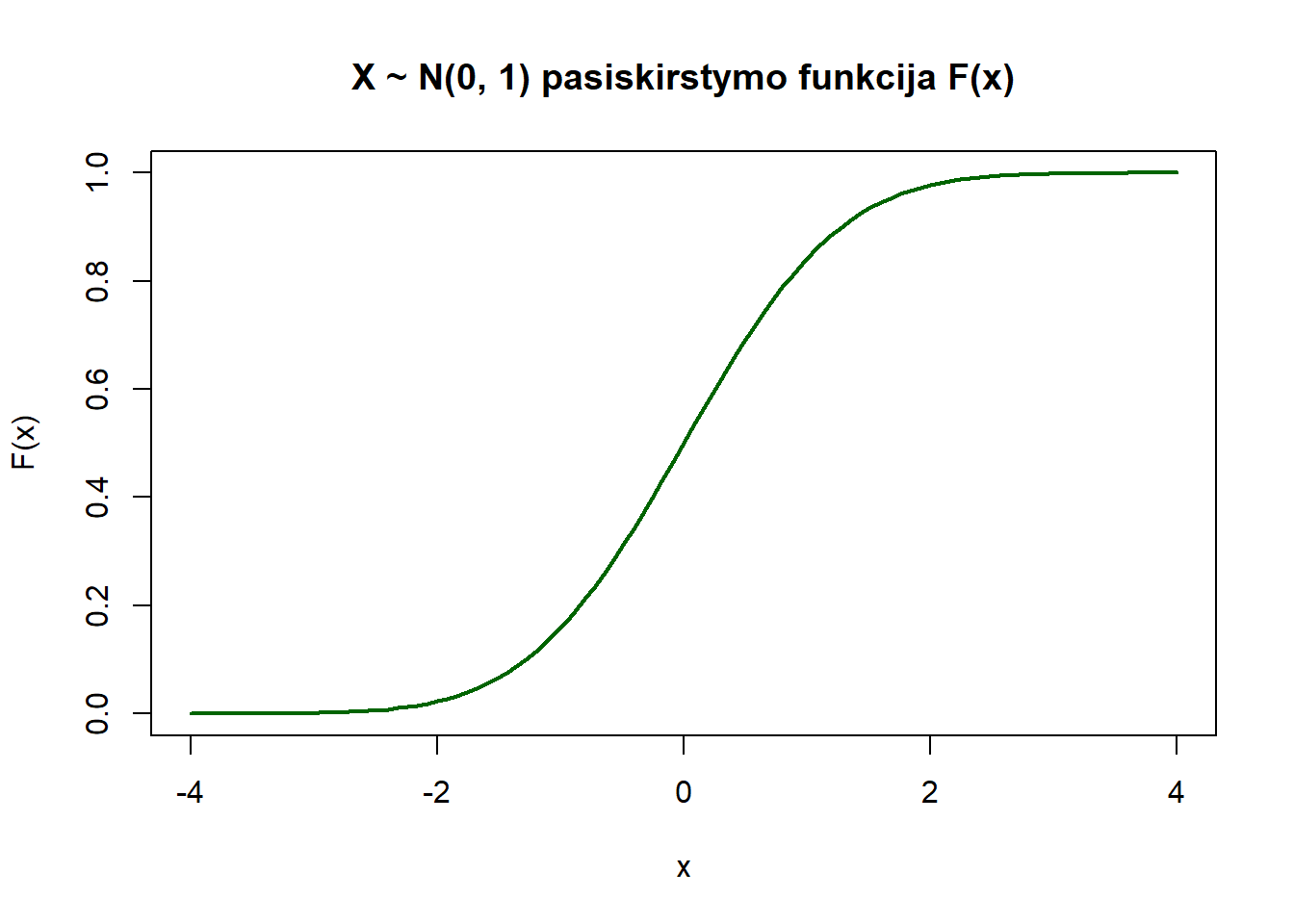

Jeigu norime parinkti kitus pasiskirstymo dėsnio parametrus (pvz. kitą vidurkio ar dispersijos reikšmę), tai galima padaryti taip:

Kodas
curve(pnorm(x, mean = 1, sd = 0.5), 
      from = -4, to = 4, ylab = "F(x)", col = "darkgreen", lwd = 2,
      main = "X ~ N(1, 0.25) pasiskirstymo funkcija F(x)")

Tankio funkcija

Tarkime, atsitiktinis dydis \(X \sim Bin(n = 10, p = 0.3)\).
Tikimybių masės funkcija apibrėžiama taip:

\[ p(x) = P(X = x) = \binom{n}{x} p^x (1-p)^{n-x}. \]

Šią funkciją galima apskaičiuoti su dbinom():

Kodas
x <- 0:10
f_binom <- dbinom(x, size = 10, prob = 0.3)
f_binom
#>  [1] 0.0282475249 0.1210608210 0.2334744405 0.2668279320 0.2001209490
#>  [6] 0.1029193452 0.0367569090 0.0090016920 0.0014467005 0.0001377810
#> [11] 0.0000059049

Šios reikšmės parodo, kokia yra tikimybė gauti konkrečią sėkmių skaičiaus reikšmę \(x\). Norėdami pavaizduoti šią funkciją, galime nubrėžti stulpelinę diagramą:

Kodas
barplot(f_binom, names.arg = x,
        main = "Binominio skirstinio tankio (tikimybių masės) funkcija",
        xlab = "x", ylab = "P(X = x)",
        col = "steelblue"
        )

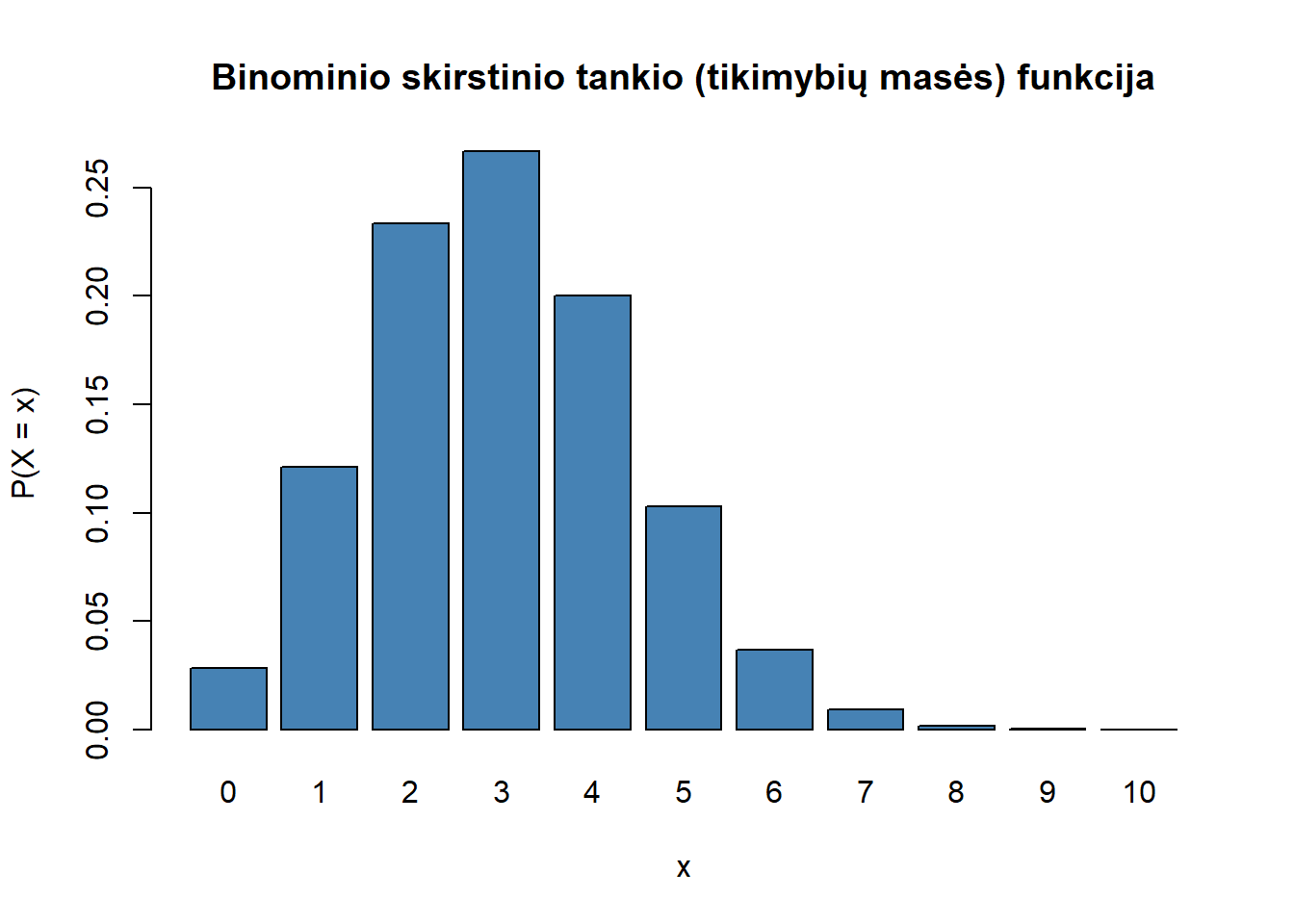
Gauname diskrečiojo a.d. tankio funkcijos grafiką, kuris parodo tikimybes kiekvienai galimai reikšmei \(x\).

Tolydžiojo atsitiktinio dydžio \(X \sim \mathcal{N}(\mu, \sigma^2)\) tankio funkcija yra:

\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-(x-\mu)^2 / 2\sigma^2} \] Tankis nusako, kaip tikimybės pasiskirsto pagal a.d. \(X\) įgyjamas reikšmes – plotas po tankio kreive tarp dviejų taškų \(a\) ir \(b\) atitinka tikimybę, kad \(X\) pateks į intervalą \([a, b)\).

R kalboje tankio funkcijos reikšmės gaunamos funkcija dnorm():

Kodas
x <- seq(-4, 4, by = 0.1)
f_norm <- dnorm(x, mean = 0, sd = 1)

Nubraižome normaliojo skirstinio tankio funkciją:

Kodas
plot(x, f_norm, type = "l", main = "Normaliojo skirstinio tankio funkcija",
xlab = "x", ylab = "f(x)", col = "darkgreen", lwd = 2)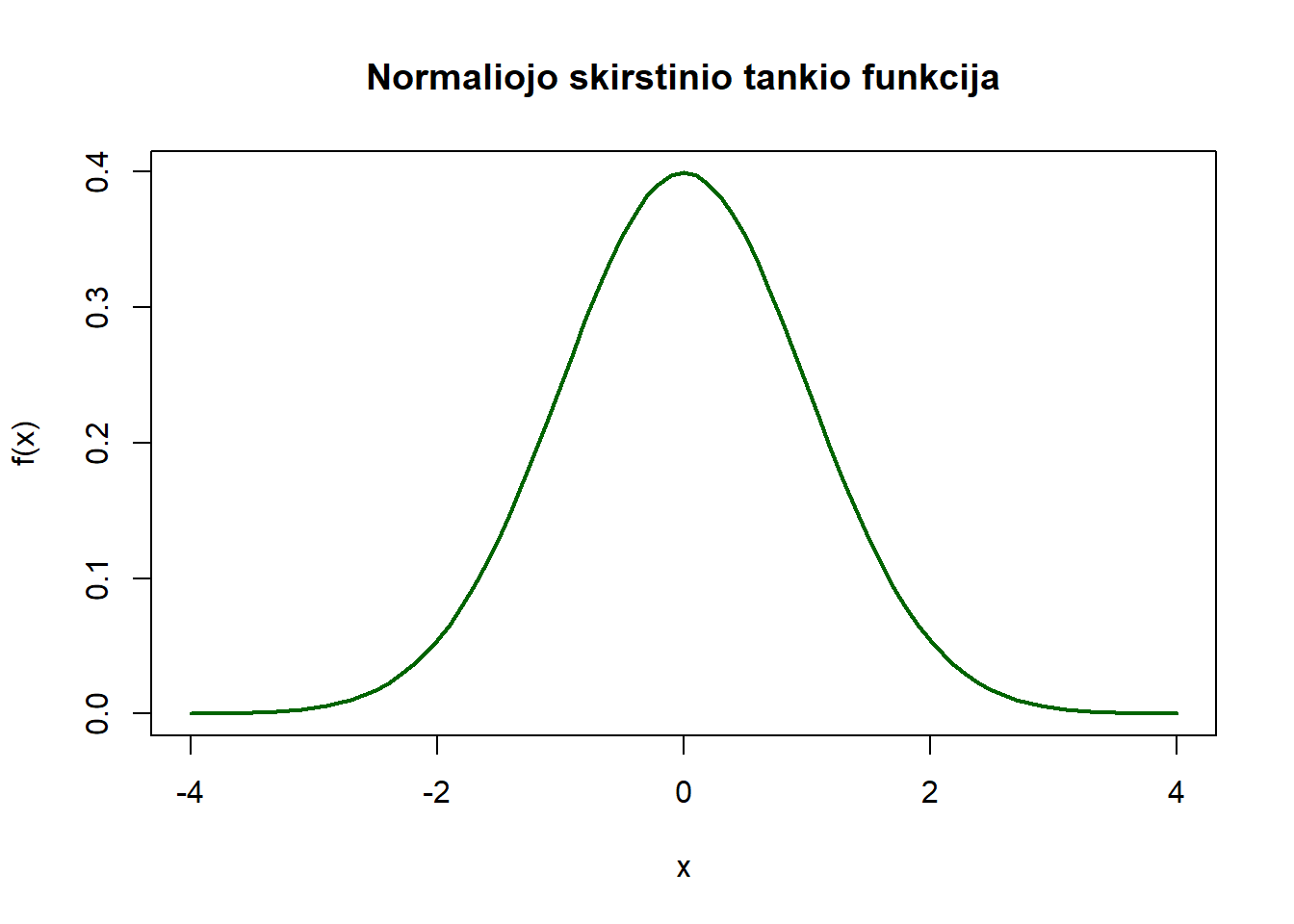

Tankio funkcijos forma priklauso nuo jos parametrų \(\mu\) (vidurkio) ir \(\sigma\) (standartinio nuokrypio). Galime palyginti kelias skirtingas parametrų reikšmes.

Kodas
curve(
  dnorm(x, mean = 0, sd = 1), from = -5, to = 5,
  ylab = "f(x)", col = "darkgreen", lwd = 2, ylim = c(0, 0.8),
  main = "Normaliojo skirstinio tankio funkcijos su skirtingomis dispersijomis"
)

curve(dnorm(x, mean = 0, sd = 0.5), add = TRUE, col = "blue", lwd = 2)
curve(dnorm(x, mean = 0, sd = 2), add = TRUE, col = "red", lwd = 2)
legend("topright", legend = c("σ = 1", "σ = 0.5", "σ = 2"),
col = c("darkgreen", "blue", "red"), lwd = 2, bty = "n")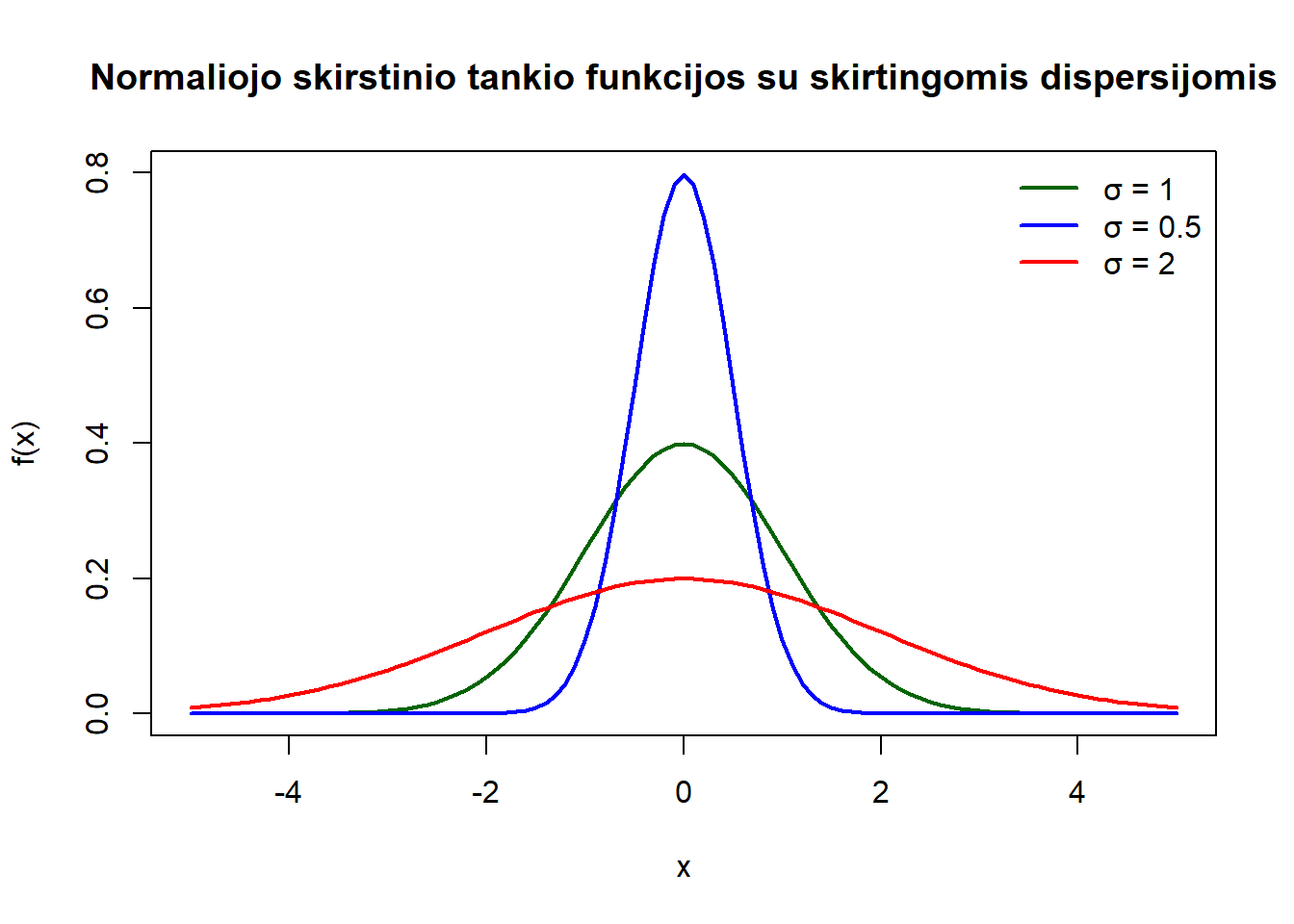

Užduotis

  1. Suskaičiuokite įvykio \(\{X = 5\}\) tikimybę, kai \(X \sim Bin(n = 20, p = 0.2)\).

  2. Suskaičiuokite įvykio \(\{X < 3\}\) tikimybę, kai \(X \sim \mathcal{N}(\mu=1, \, \sigma^2 = 4)\).

  3. Suskaičiuokite įvykio \(\{X \geq 3\}\) tikimybę, kai \(X \sim \mathcal{N}(\mu=1, \, \sigma^2 = 4)\).

  4. Suskaičiuokite įvykio \(\{1 \leq X \leq 3\}\) tikimybę, kai \(X \sim \mathcal{N}(\mu=1, \, \sigma^2 = 4)\).

  5. Naudojant funkciją integrate(), suskaičiuokite tikimybę \(P(0.14 \leq X \leq 0.71)\), kai a.d. \(X\) tankio funkcija yra \(f(x) = 3x^2, \,\, 0<x<1.\)

Atsitiktinių dydžių generavimo funkcijos

Kadangi R programavimo kalba yra sukurta statistikams, joje galima rasti daug funkcijų, skirtų generuoti atsitiktinius dydžius - arba iš nurodyto reikšmių vektoriaus, arba iš egzistuojančių pasiskirstymo dėsnių.

Imtimi vadinsime atrinktų vienetų dalį iš juos vienijančios populiacijos, kitaip tariant tai populiacijos poaibis. Imtys gali būti atsitiktinės, pseudoatsitiktinės arba deterministinės.

Atsitiktinės imties iš vektoriaus elementų sudaryimui naudojama funkcija sample().

Argumentas Reikšmė
x vektorius, iš kurio renkamos imties reiškmės
size iš vektoriaus x išrenkamų elementų skaičius (imties dydis)
replace loginis, nurodo, ar išrenkami elementai gali kartotis
prob išrenkamų elementų tikimybės, pagal nutylėjimą jos vienodos

Pavyzdžiui, iš 5 elementus turinčios aibės \(x = \{1, 2, 3, 4, 5\}\) atsitiktine tvarka su vienodomis tikimybėmis išrinksime 3 elementus.

Kodas
x <- 1:5
n <- 3
sample(x, size = n)
#> [1] 3 2 4

# arba kompaktiškiau
sample(x, n)
#> [1] 1 3 5

Jeigu nenurodamas imties dydis, atliekamas vektoriaus elementų išdėstymas atsitiktine tvarka.

Kodas
sample(x)
#> [1] 1 5 4 3 2

Jeigu parametro x reikšmė yra ne vektorius, bet tik vienas natūrinis skaičius \(m\), tai imtis bus renkama iš vektoriaus \((1, 2, ..., m)\) elementų.

Kodas
sample(x, size = 3)
#> [1] 1 3 5

Pagal nutylėjimą funkcija sample() sudaro paprastąją atsitiktinę negrąžintinę imtį, todėl imties elementai nesikartoja. Jeigu imties elementai gali kartotis arba išrenkamų elementų skaičius didesnis už vektoriaus elementų skaičių, loginis parametras replace = TRUE.

Kodas
sample(x = 1:3, size = 5, replace = TRUE)
#> [1] 1 1 1 1 1

Taip pat pagal nutylėjimą visų vektoriaus x elementų išrinkimo tikimybės vienodos, tačiau jas galima keisti - parametrui prob priskirti elementų išrinkimo tikimybių vektorių. Šis vektorius turi būti tokio paties ilgio kaip ir x vektorius, o tikimybių suma turi būti lygi vienetui.

Pvz., iš aibės \(x = \{1, 2, 3, 4, 5\}\) išrinksime atsitiktinę \(k = 1000\) dydžio imtį. Kadangi visų aibės elementų išrinkimo į imtį tikimybės vienodos ir lygios \(1/5\), tokiu būdu sudarytoje imtyje elementų skaičius turi būti maždaug vienodas ir lygus apie 200.

Kodas
n <- 1000
imtis <- sample(x, n, replace = TRUE)

table(imtis)
#> imtis
#>   1   2   3   4   5 
#> 177 197 213 219 194
barplot(table(imtis))

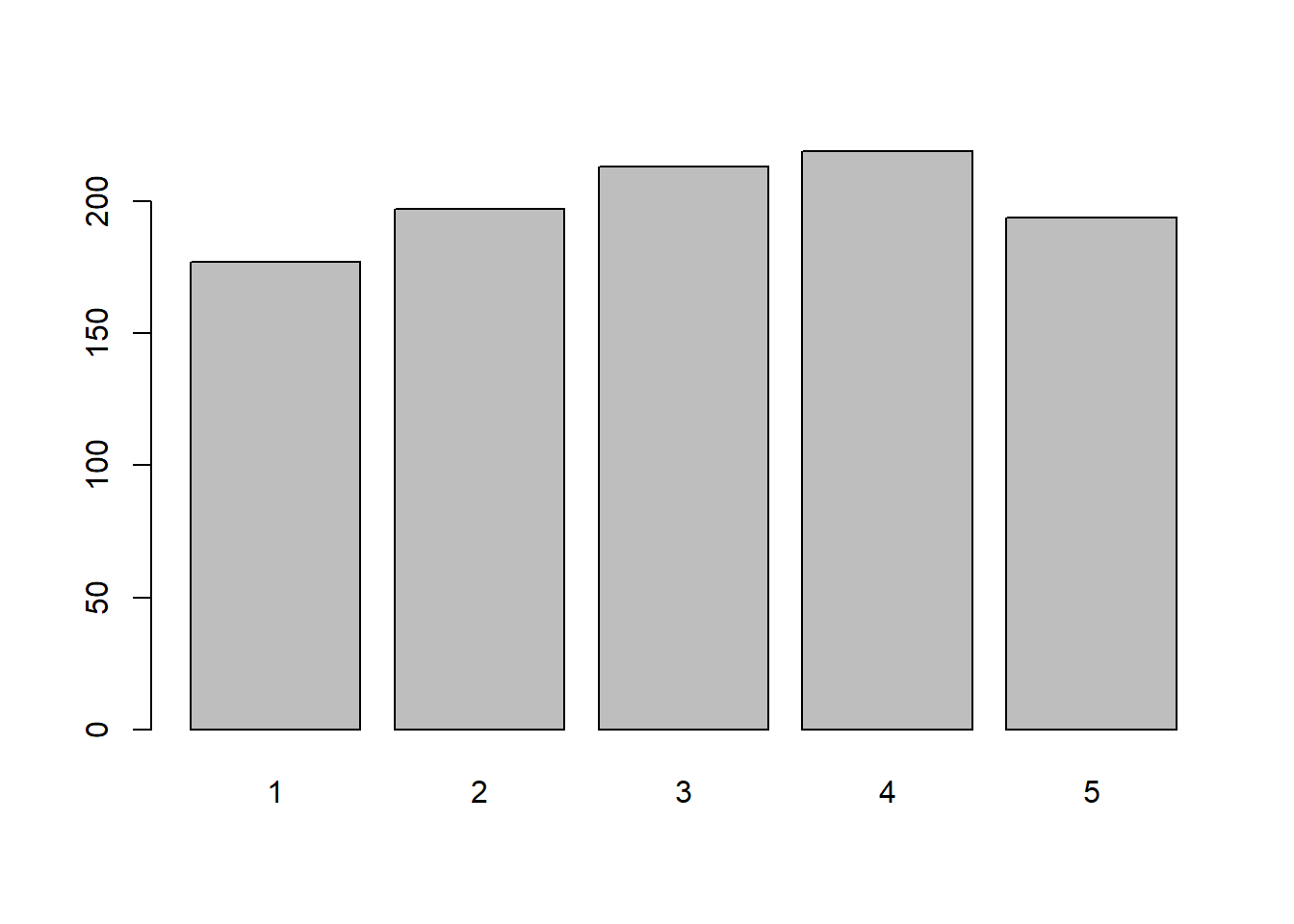
Dabar išrinkimo tikimybes pakeisime taip, kad pirmas ir paskutinis aibės elementai būtų išrenkami su tikimybe \(0.1\), antras ir ketvirtas su tikimybe \(0.2\), o trečias – su tikimybe \(0.4\). Vadinasi, gautoje imtyje tečio elemento turėtų būti apie 400, antro ir ketvirto apie 200, o pirmo ir paskutinio po 100.

Kodas
n <- 1000
p <- c(0.1, 0.2, 0.4, 0.2, 0.1)

imtis <- sample(x, n, replace = TRUE, prob = p)
table(imtis)
#> imtis
#>   1   2   3   4   5 
#>  76 209 408 198 109

Visiems atsitiktinių dydžių generatoriams galima nurodyti pradinę generuojamos sekos reikšmę, kuri vadinama seed. Su ta pačia seed reikšme gaunama tokia pati skaičių seka.

Suprantama, kad atsitiktinių dydžių seka, kurią galima atkartoti, nėra atsitiktinė, todėl tokiu būdu gauti dydžiai vadinami pseudoatsitiktiniais. Šią generatorių savybę galima naudoti tuo atveju, kai reikia visiškai tiksliai atkartoti tikimybinio modeliavimo eksperimentą.

Generatoriui seed reikšmė nustatome per funkciją set.seed(), kuriai nurodomas sveikasis skaičius, kuris ir reiškia seed reikšmę.

Kodas
set.seed(666)
sample(5)
#> [1] 3 5 2 1 4

Norint gauti tą pačią a.d. seką, seed reikšmę reikia nurodyti iš naujo prieš kiekvieną kartą naudojant a.d. generavimo funkciją.

Kodas
# gauname skirtingas a.d. sekas
sample(5)
#> [1] 4 1 2 5 3
sample(5)
#> [1] 5 3 4 2 1
Kodas
# gauname tą pačią a.d. seką
set.seed(666)
sample(5)
#> [1] 3 5 2 1 4

set.seed(666)
sample(5)
#> [1] 3 5 2 1 4

Atsitiktinių dydžių generavimui pagal pasirinktą pasiskirstymo dėsnį, naudojamos r*() funkcijos, kur vietoje * reikia nurodyti dėsnio pavadinimą, pvz. rnorm, runif, ar rpois.

Pagrindinis tokių funkcijų argumentas yra atsitiktinės imties dydis n, o kiti argumentai reikalingi pasiskirstymo dėsnio parametrams nusakyti.

Kodas
# standartinio normaliojo a.d.
imtis_norm <- rnorm(n = 1000)
mean(imtis_norm)
#> [1] 0.05212823
sd(imtis_norm)
#> [1] 0.9806363

# Puasono a.d.
imtis_pois <- rpois(n = 1000, lambda = 5)
mean(imtis_pois)
#> [1] 5.015
var(imtis_pois)
#> [1] 4.833609
Užduotis

  1. Naudodami funkciją sample(), parašykite loterijos skaičių generavimo komandą, kuri iš 30 sunumeruotų kamuoliukų be pasikartojimų ištrauktų 6.

  2. Parašykite antrą loterijos programos pusę, kuri tokiu pačiu būdu parinktų 6 žaidėjo skaičius ir apskaičiuotų, kiek iš jų sutampa su loterijos skaičiais.

  3. Užrašykite komandą, kuri vektoriaus LETTERS elementus išdėliotų atsitiktine tvarka.

  4. Užrašykite komandą, kuri atsitiktine tvarka sudėliotų duomenų lentelės iris eilutes.

  5. Sumodeliuokite simetriško šešiasienio lošimo kauliuko mėtymą. Sugalvokite komandą, kuri modeliuotų iš karto 100 lošimo kauliukų metimą.

  6. Kaip mėtant lošimo kauliuką galima imituoti monetos mėtymą? Užrašykite tokį procesą modeliuojantį algoritmą.

  7. Sumodeliuokite dviejų simetriškų monetų \(n = 100\) metimų seriją ir sudarykite visų kombinacijų atsivertimų dažnių lentelę. Ar visos kombinacijos pasirodo vienodai dažnai?

  8. Tarkime, kad \(X\) yra bendra taškų suma metant du simetriškus lošimo kauliukus. Modeliavimo būdu nustatykite, kokia suma pasitaiko dažniau, \(X = 9\) ar \(X = 10\)?

17.3 Aprašomoji statistika