10  Kelių grafikų viename grafiniame lange braižymas

Kai iškviečiame aukšto lygio funkciją, pvz. plot(), hist(), barplot(), R atveria naują grafinį langą (arba išvalo seną) naudodama vidinę funkciją plot.new(). Norėdami rankiniu būdu atverti langą Windows operacinėje sistemoje, galime kviesti windows() funkciją.

windows()
plot.new()

Tačiau viename lange vienu metu rodoma tik vienas grafikas.

10.1 Grafiniai parametrai mfrow ir mfcol

Jeigu norime tame pačiame lange turėti kelis grafikus, langą reikia padalyti į keletą dalių. Patogiausia naudoti grafinius parametrus: mfrow ir mfcol. Įvykdžius komandas, kurios iškviečia šių grafinių parametrų reikšmes, galima pamatyti į kiek dalių vienas grafinis langas yra išskaidytas: mfrow nurodo eilučių skaičių, o mfcol - stulpelių.

par("mfrow")
#> [1] 1 1
par("mfcol")
#> [1] 1 1

Atkreipkite dėmesį, jog funkcijoje par() grafinių parametrų reikšmės nurodytos kaip simboliai.

Parametro reikšmę galime keisti taip:

• par(mfrow = c(nr, nc)) – langas dalijamas eilutėmis, t. y. grafikai pildomi iš kairės į dešinę, po to pereinama į kitą eilutę žemiau (eilutė po eilutės);

• par(mfcol = c(nr, nc)) – langas dalijamas stulpeliais, t. y. grafikai pildomi iš viršaus į apačią, po to pereinama į kitą stulpelį dešiniau (stulpelis po stulpelio).

Čia nr ir nc atitinkamai reiškia eilučių ir stulpelių skaičių.

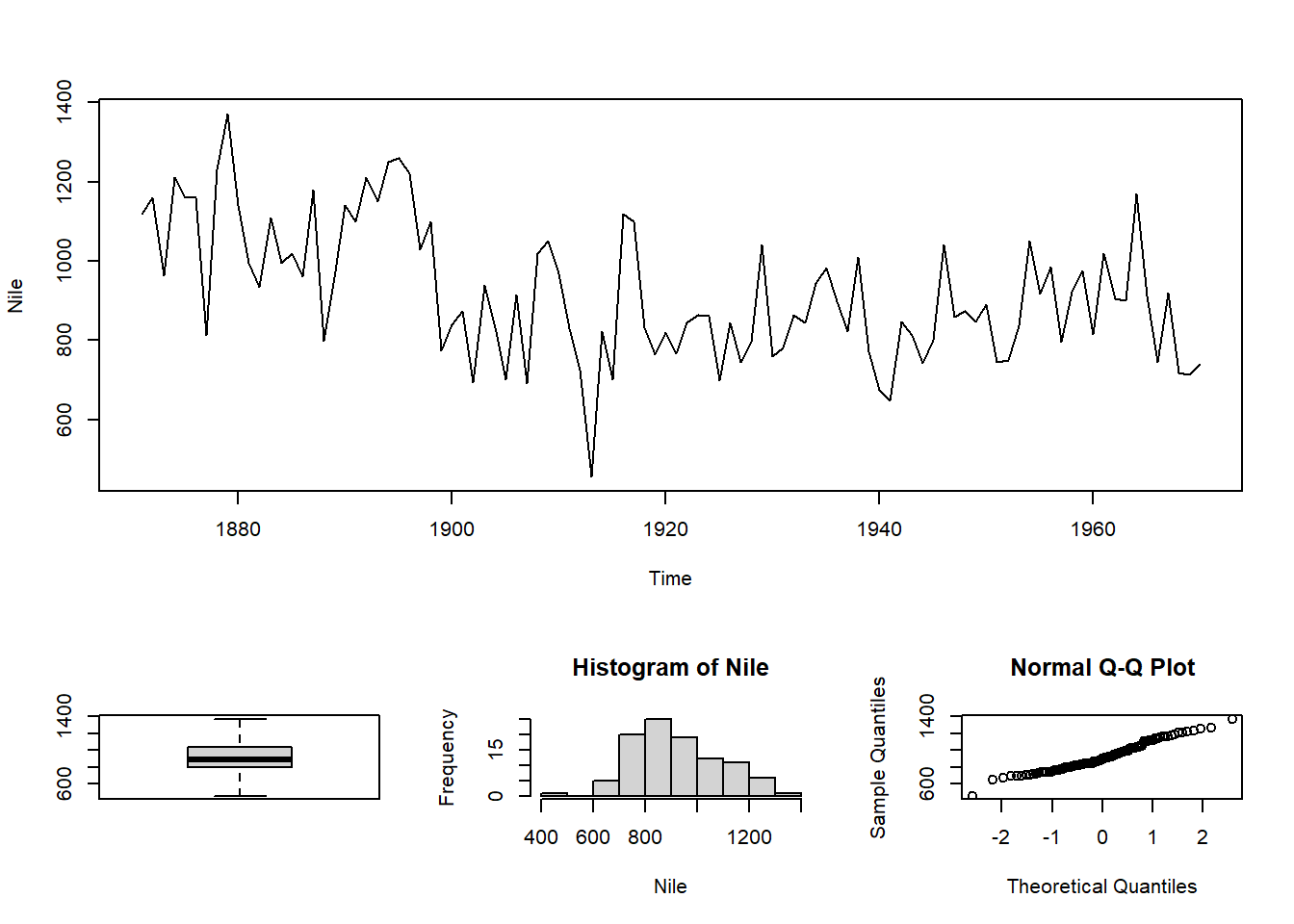
Pavyzdžiui, grafinį langą padalinsime vertikaliai į dvi dalis, nubraižysime du skirtingus grafikus.

par(mfrow = c(1, 2))

plot(Temp ~ 1, data = airquality, pch = 20, frame = FALSE)
boxplot(Temp ~ Month, data = airquality, frame = FALSE)

Naudinga

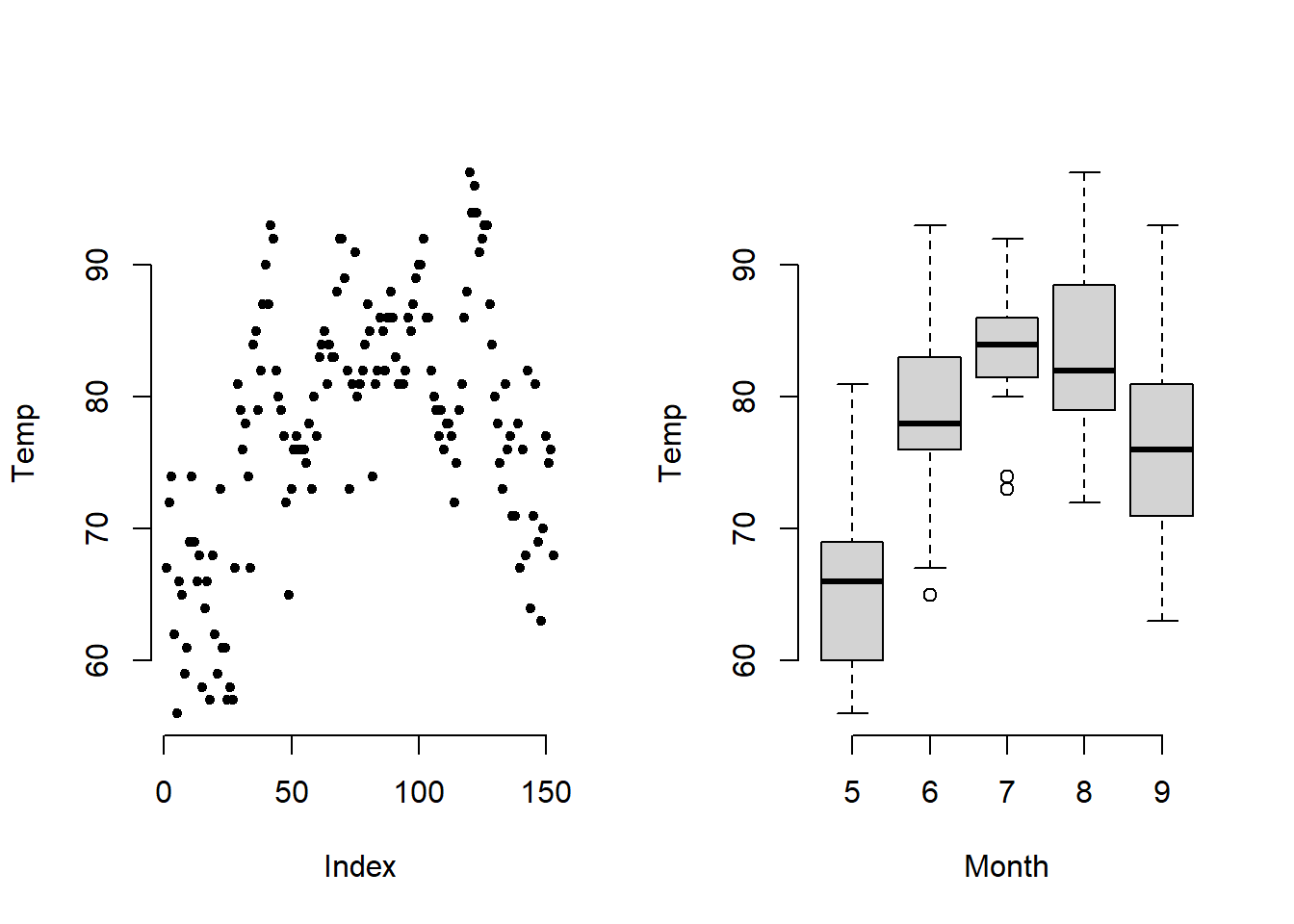
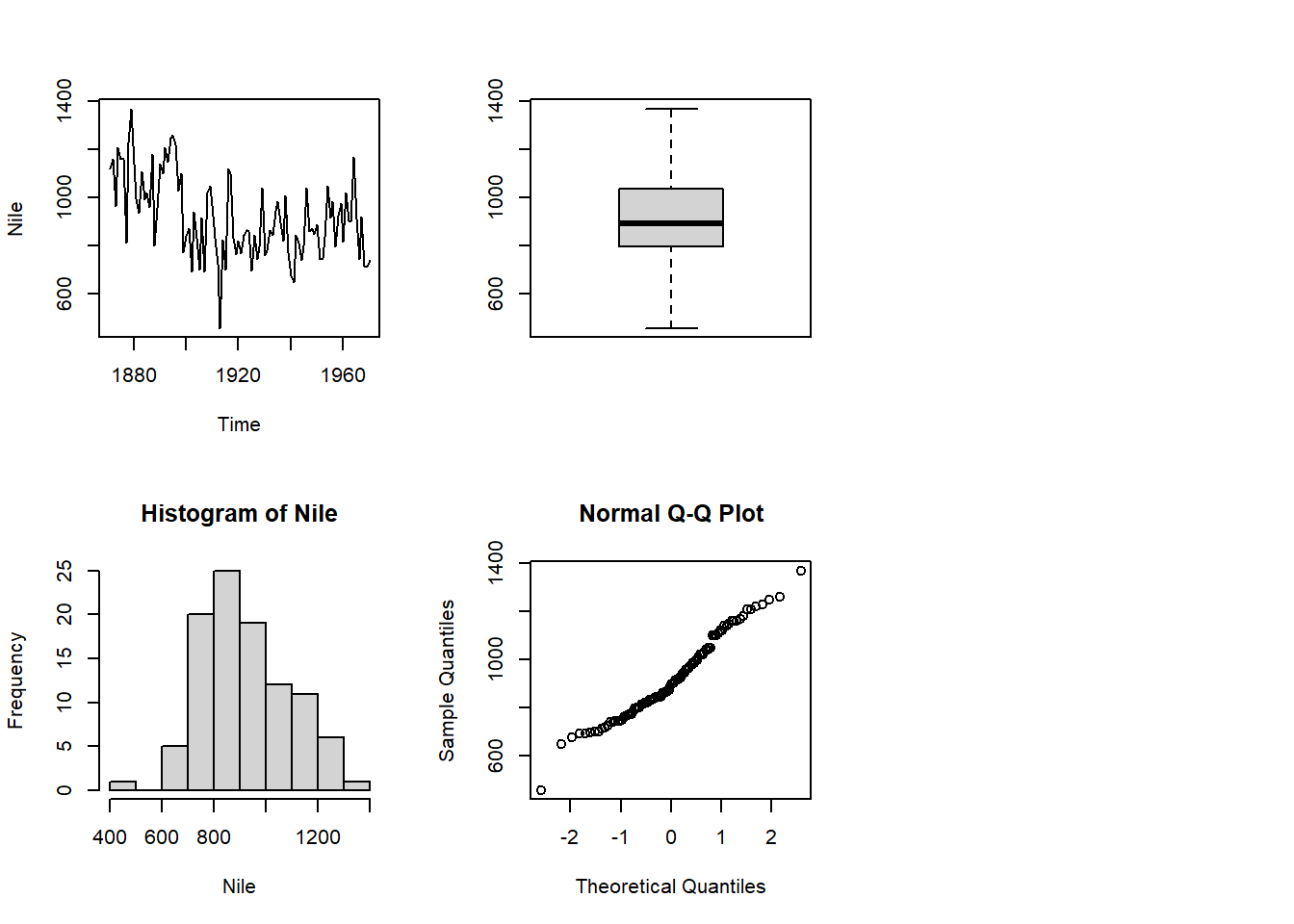
Dažnai tenka nagrinėti ir tarpusavyje palyginti daug tokio paties tipo grafikų. Tam, kad visi grafikai būtų matomi vienu metu, juos galima nubraižyti į keletą dalių sudalintame grafiniame lange. Tarkime, kad eksperimentas kartojamas 25 kartus. Reikia nubraižyti kiekvieno bandymo matavimų histogramas. Čia duomenys duoti matricos pavidalu.

duomenys <- replicate(25, rnorm(200, sample(20, 1)))

Naują grafinį langą padaliname į 25 mažesnius langus. Papildomai nurodome visų langų paraščių pločius.

par(mfrow = c(5, 5), mar = c(2, 2, 1, 1))

Apskaičiuojame grafiko ašių ribas.

xx <- round(range(duomenys) + c(-0.5, 0.5))
yy <- c(0, 60)

Funkciją hist() naudojame su kiekvienu stulpeliu atskirai. Tokį daug pakartojimų reikalaujantį veiksmą galima įdėti į ciklą for arba naudoti apply() funkciją.

apply(duomenys, 2, \(x) hist(x, breaks = 10, xlim = xx, ylim = yy, ann = FALSE))

Užduotis

Sąlyga

1. Viename lange nubraižykite keturias kreives - \(\sin x\), \(\cos x\), \(\mathrm{tg}(x+2)\), \(\mathrm{e}^{iz}\) intervale \([-\pi, \pi]\). Grafikus užpildykite pagal stulpelius.

2. Padalinkite langą į \(1 \times 3\) dalis ir nubraižykite iris duomenų lentelės kintamųjų Sepal.Length, Sepal.Width, Petal.Length histogramas.

10.2 Funkcija layout()

Jeigu grafinis langas padalinamas į dalis naudojant grafinius parametrus mfrow arba mfcol, visos tos dalys yra vienodo dydžio. Be to, negalima nustatyti jų užpildymo tvarkos. Tokie apribojimai kartais gali sukelti nepatogumų. Jų galima išvengti naudojant funkciją layout().

Argumentas	Reikšmė
mat	matrica, kurios elementai nurodo lango dalių užpildymo tvarką
widths	grafinio lango stulpelių pločių vektorius
heights	grafinio lango eilučių aukščių vektorius

Ši funkcija leidžia sukurti grafinio lango padalijimo į dalis plano matricą ir nustatyti stulpelių bei eilučių proporcijas.

Plano matricos reikšmės gali būti 0 arba teigiami sveikieji skaičiai. Tas pats skaičius reiškia, kad lango dalys bus sujungtos į vieną. Reikšmė 0 žymi, kad atitinkama lango dalis nebus naudojama.

Pavyzdžiui, tarkime, kad grafinį langą reikia padalinti į dvi eilutes bei tris stulpelius, o jų užpildymo tvarką nusako tokia matrica:

\[\begin{equation} \begin{bmatrix} & & & & & & \\ & 1 & & 2 & & 5 & \\ & & & & & & \\ & 3 & & 4 & & 6 & \\ & & & & & & \end{bmatrix} \end{equation}\]

Sudarome \(2 \times 3\) dydžio grafikų išdėstymo plano matricą.

m <- matrix(c(1, 2, 5, 3, 4, 6), nrow = 2, ncol = 3, byrow = TRUE)

layout(mat = m)

Grafiniame lange galima parodyti atskirų langų numerius naudojant funkciją layout.show().

layout.show(6)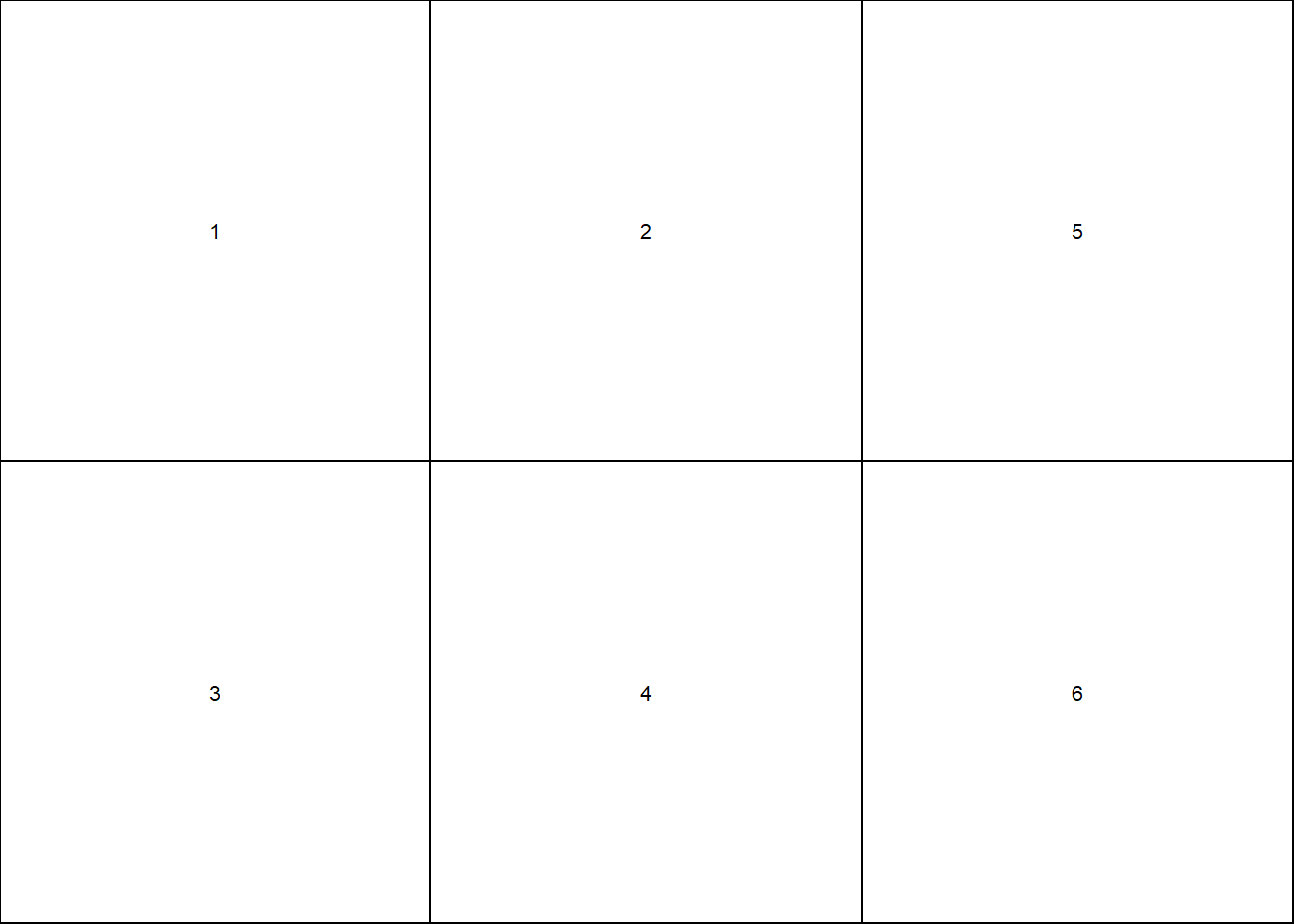

Galiausiai nubraižome keturis statistinius grafikus, kurie grafiniame lange išdėstomi pagal duotos plano matricą.

plot(Nile)
boxplot(Nile)
hist(Nile)
qqnorm(Nile)

Sudarysime kitą padalinimo plano matricą ir atvaizduosime tuos pačius keturis grafikus.

# Kitas išdėstymas:
#    +----+----+----+
#    |      1       |
#    +----+----+----+
#    | 2  | 3  | 4  |
#    +----+----+----+

i <- c(1, 1, 1, 2, 3, 4)
m <- matrix(i, nrow = 2, ncol = 3, byrow = TRUE)

layout(m)

plot(Nile)
boxplot(Nile)
hist(Nile)
qqnorm(Nile)

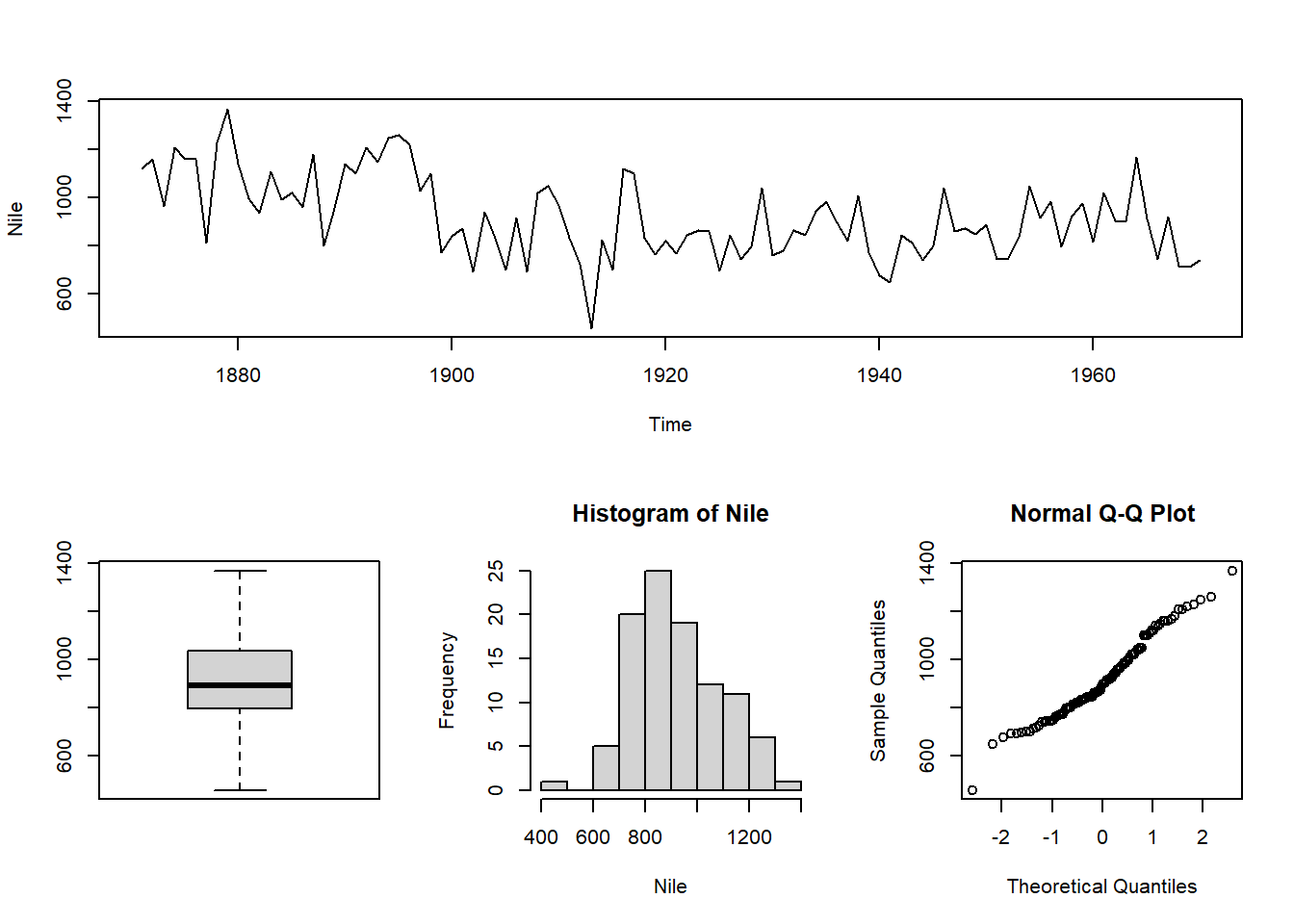
Jeigu parametrų widths ir heights reikšmės nenurodomos, tai santykinis eilučių ir stulpelių plotis pagal nutylėjimą yra vienodas ir lygus 1.

Šį santykį galima keisti. Pvz., jeigu viena eilutė turi būti du kartus platesnė už kitą, tada jos pločio koeficientas taip pat turi būti du kartus didesnis už kitos eilučių pločio koeficientą.

Tęsiant paskutinį pavyzdį, antros eilutės plotą padarysime dvigubai mažesnį, o stulpelių pločiai tegul lieka vienodi.

layout(m, heights = c(2, 1))

plot(Nile)
boxplot(Nile)
hist(Nile)
qqnorm(Nile)

Naudinga

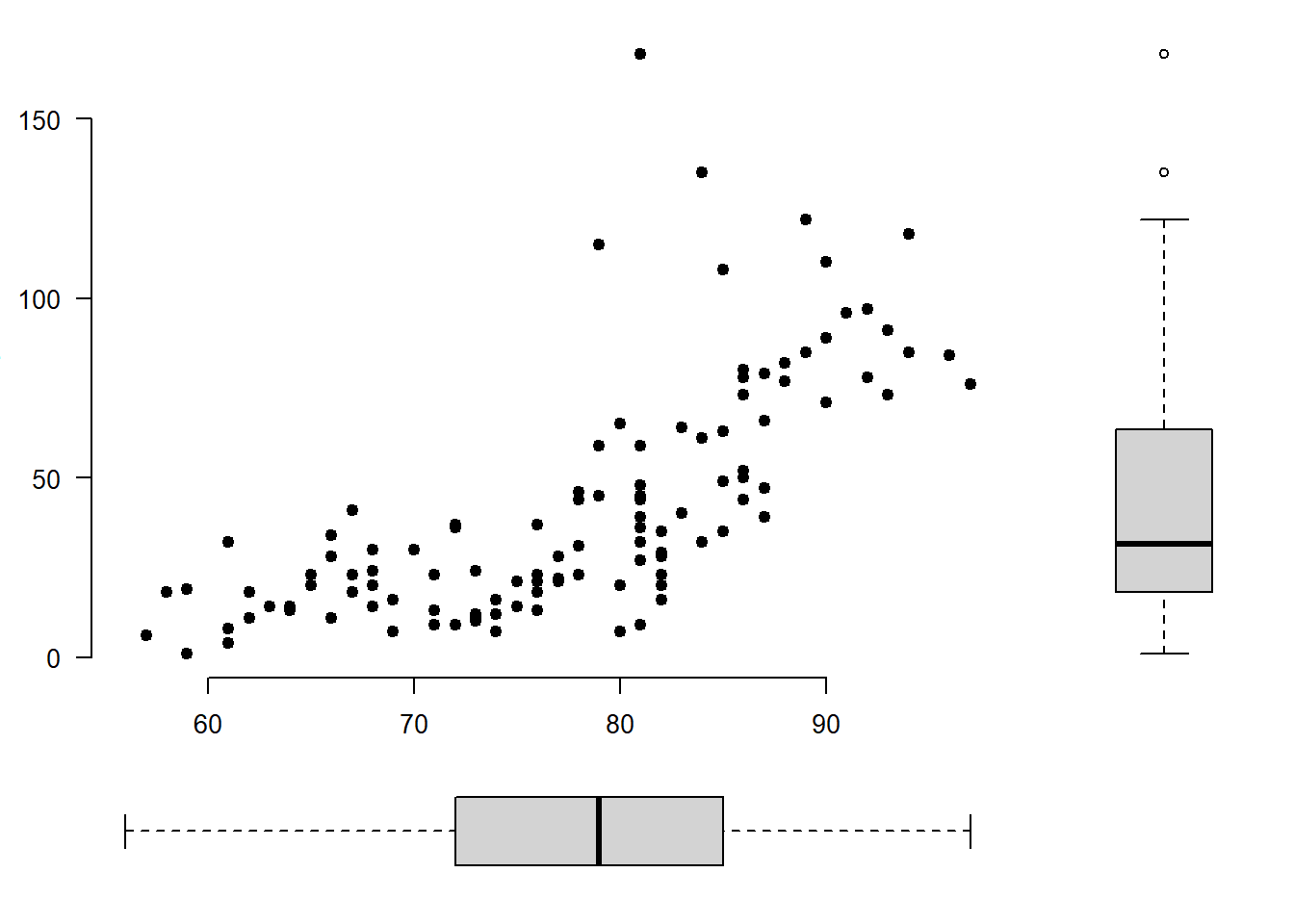
Grafinį langą suskirstant į keletą įvairaus dydžio dalių, galima sudaryti gana sudėtingą diagramą. Pavyzdžiui, nubraižysime dviejų kintamųjų sklaidos grafiką ir šalia nubraižysime atskirai vieno ir kito kintamojo stačiakampes diagramas.

Grafinį langą suskirstysime į 4 dalis: pagrindinėje dalyje braižomas kintamųjų \(x\) ir \(y\) sklaidos grafikas, antroje ir trečioje stačiakampės diagramos, ketvirta dalis nenaudojama. Kadangi stačiakampės diagramos siauros, tai antra eilutė ir antras stulpelis bus 4 kartus siauresni nei pirma eilutė ir pirmas stulpelis.

layout(matrix(c(1, 2, 3, 0), 2, 2), widths = c(4, 1), heights = c(4, 1))
layout.show(3)

x <- airquality$Temp
y <- airquality$Ozone

Pirmiausia nubraižome pagrindinę sklaidos diagramą. Nustatome paraščių pločius.

par(mar = c(2, 3, 1, 1))
plot(x, y, pch = 19, frame = FALSE, las = 1)

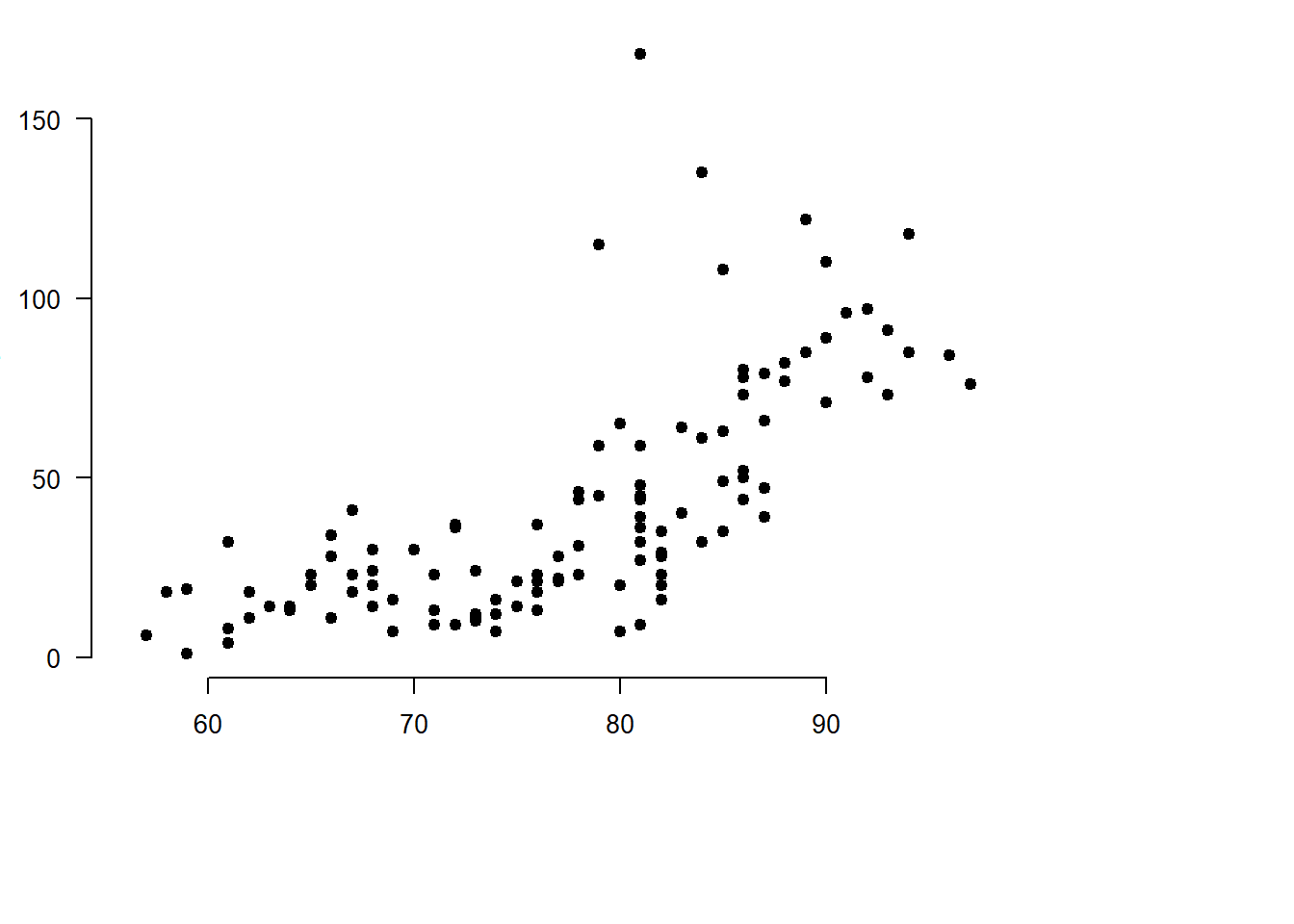
Atskiros grafinio lango dalys yra nesusijusios. Kad iš keleto grafikų sudaryta diagrama būtų teisinga, turi sutapti atskirų grafikų koordinačių ašys. Pvz., apačioje braižomos diagramos \(Ox\) ašis turi sutapti su pagrindinio grafiko \(Ox\) ašimi. šiuo atveju užtenka nustatyti vienodas paraštes iš kairės ir dešinės. Kadangi ašys sutapatintos, nurodome, kad naujame grafike ašys nebūtų braižomos.

par(mar = c(0, 3, 0, 1))
boxplot(x, frame = FALSE, axes = FALSE, horizontal = TRUE)

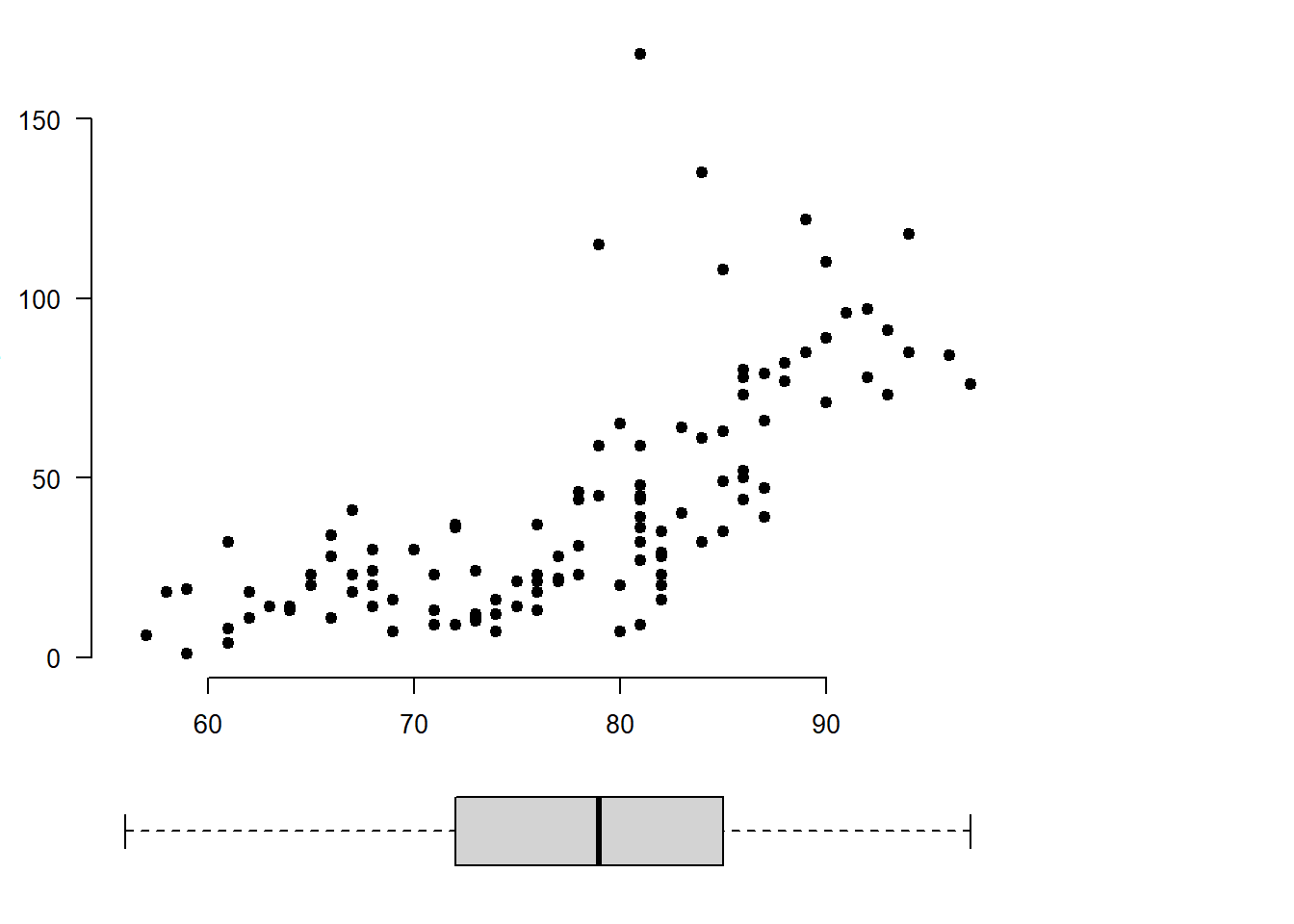
Kad sutaptų pagrindinio ir šoninio grafiko \(Oy\) ašys, nustatome vienodą paraščių plotį iš apačios ir viršaus. Kaip ir ankstesniu atveju, ašių nebraižome.

par(mar = c(2, 0, 1, 0))
boxplot(y, frame = FALSE, axes = FALSE)

10.3 Braižymo srities apribojimas

Jeigu grafike naudojamos žemo lygio funkcijos, jų braižymo sritis atitinka aukšto lygio grafiko braižymo sritį. Tačiau grafiko sritį, kurioje bus matomas ant viršaus uždedamas kitas grafikas, galima keisti. Tam naudojama funkcija clip(), kuri sukuria tarsi stačiakampį trafaretą. Jos parametrai nurodo to stačiakampio ribas:

• x1 – kairysis kraštas,
• x2 – dešinysis kraštas,
• y1 – apatinis kraštas,
• y2 – viršutinis kraštas.

Tarkim, kad reikia nubraižyti funkcijos \(y = \sin x\) grafiką intervale \([-\pi, \pi]\), tačiau intervale \([-2, 1]\) grafiko linija turi būti raudonos spalvos. Iš pradžių nubraižysime paprastą grafiką intervale \([-\pi, \pi]\), o tada ant viršaus uždėsime antrą kreivę – trafaretu apribotą raudonos spalvos sinusoidę.

curve(sin, -pi, pi, xlab = "x", ylab = "y", las = 1, frame = FALSE)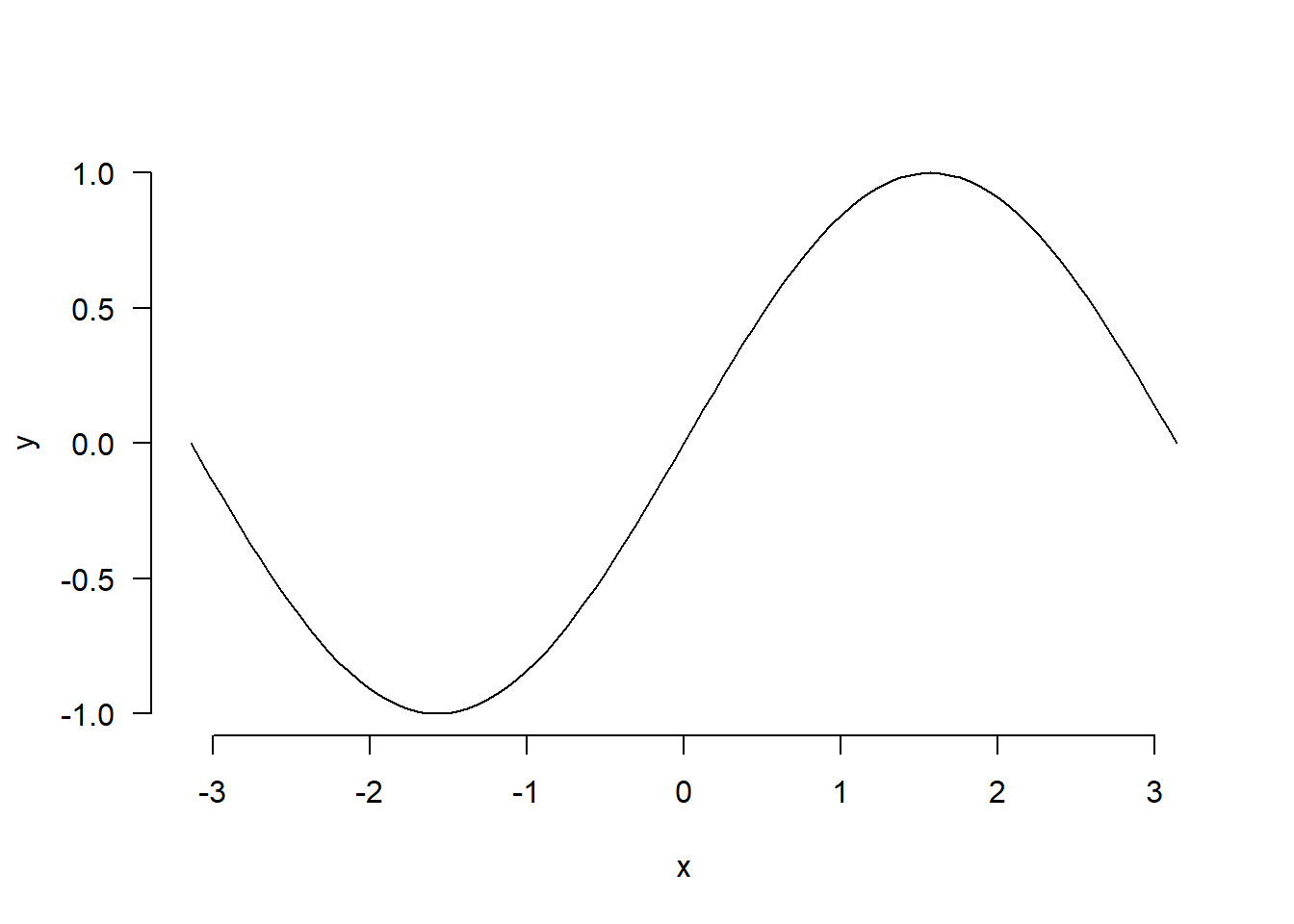

Trafareto ribos iš kairės ir dešinės žinomos, o apatinė ir viršutinė riba gali sutapti su pradinio grafiko apatine ir viršutine riba. Bet kokio grafiko ribas nurodo grafinis parametras usr. Pirmosios dvi reikšmės nurodo grafiko ribas iš kairės ir dešinės, o kitos kitos dvi – ribas iš apačios ir viršaus.

usr <- par("usr")
usr
#> [1] 0 1 0 1

Nurodome trafareto ribas. Apatinę ir viršutinę ribas paimame iš parametro usr.

clip(-2, 1, usr[3], usr[4])

Ant viršaus raudona linija braižome antrą sinusoidę. Atkreipkite dėmesį į tai, kad grafiko ribos nurodytos \([-\pi, \pi]\), bet raudona linija bus matoma tik intervale \([-2, 1]\).

curve(sin, -pi, pi, add = TRUE, col = "red", lwd = 2)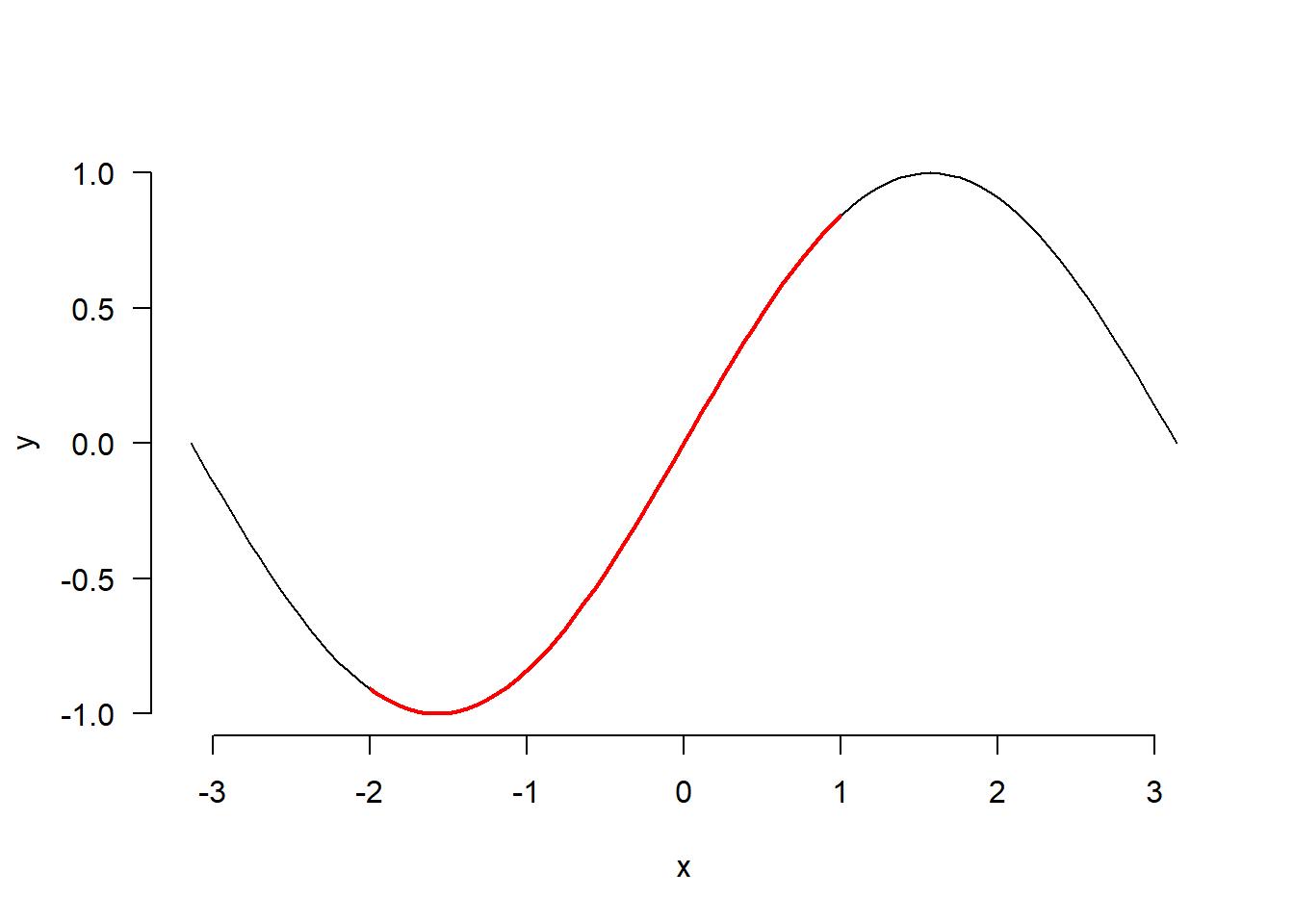

Kartą nustatytos trafareto ribos tokios ir išlieka. Pvz., ant grafiko uždėsime tinklelį, tačiau jis vis tiek bus matomas tik intervale \([-2, 1]\).

grid()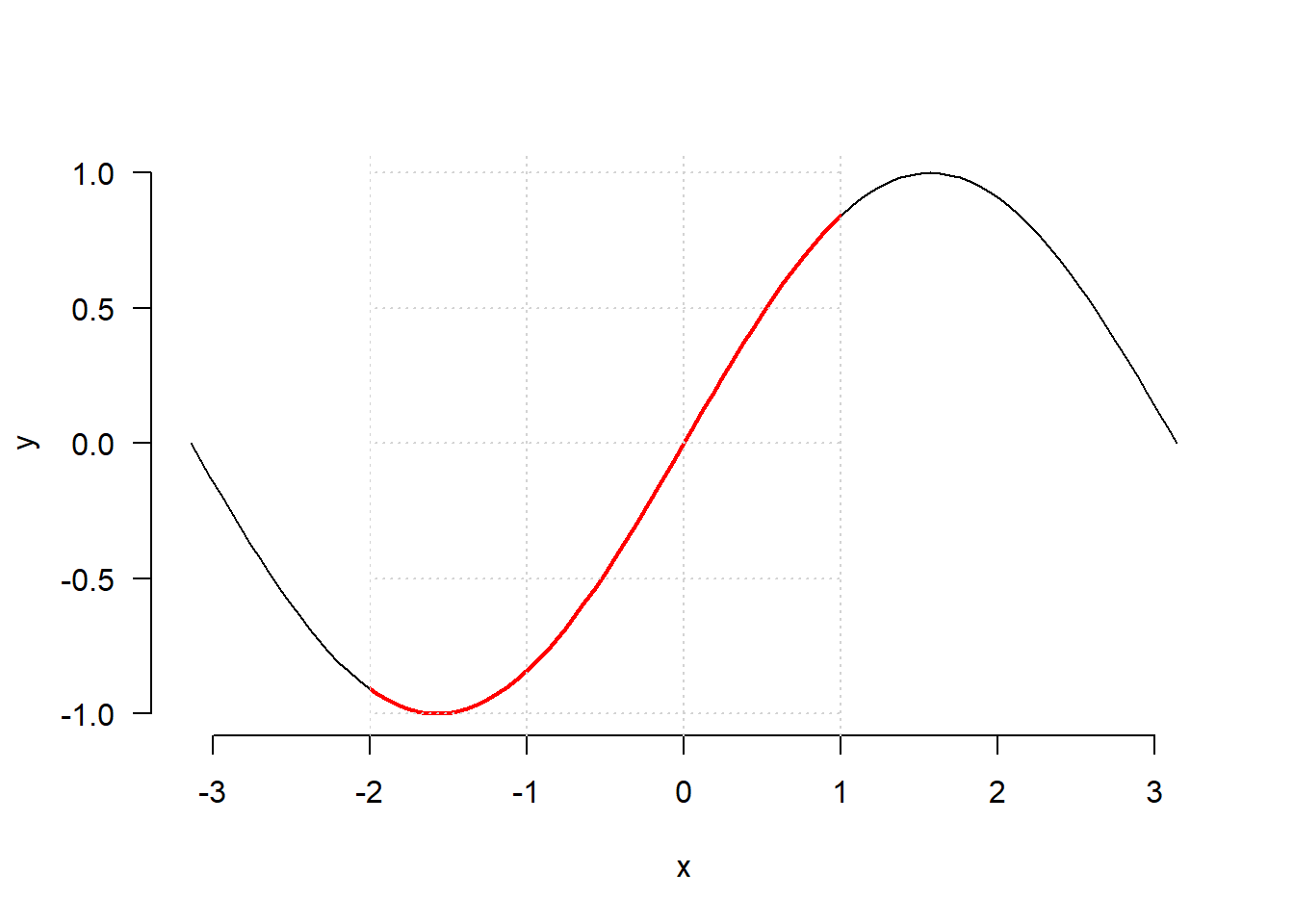

Norint sugrąžinti pradinę braižymo sritį, trafareto ribas reikėtų išplėsti iki pradinio grafiko ribų. Tam galima panaudoti prieš tai išsaugotas parametro usr reikšmes ir perduoti jas funkcijai clip() per tokią konstrukciją:

do.call(clip, as.list(usr))